题目内容
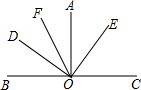 如图所示,∠AOB=∠AOC=90°,∠DOE=90°,OF平分∠AOD,∠AOE=36°.
如图所示,∠AOB=∠AOC=90°,∠DOE=90°,OF平分∠AOD,∠AOE=36°.(1)求∠COD的度数;
(2)求∠BOF的度数.
考点:余角和补角,角平分线的定义
专题:
分析:(1)先求出∠COE=54°,即可求出∠COD=∠DOE+∠COE=144°;
(2)先求出∠AOD=54°,再求出∠BOD和∠DOF,即可求出∠BOF.
(2)先求出∠AOD=54°,再求出∠BOD和∠DOF,即可求出∠BOF.
解答:解:(1)∵∠AOC=90°,
∴∠COE=90°-AOE=90°-36°=54°,
∴∠COD=∠DOE+∠COE=90°+54°=144°;
(2)∵∠DOE=90°,∠AOE=36°,
∴∠AOD=90°-36°=54°,
∵∠AOB=90°,
∴∠BOD=90°-54°=36°,
∵OF平分∠AOD,
∴∠DOF=
∠AOD=27°,
∴∠BOF=36°+27°=63°.
∴∠COE=90°-AOE=90°-36°=54°,
∴∠COD=∠DOE+∠COE=90°+54°=144°;
(2)∵∠DOE=90°,∠AOE=36°,
∴∠AOD=90°-36°=54°,
∵∠AOB=90°,
∴∠BOD=90°-54°=36°,
∵OF平分∠AOD,
∴∠DOF=
| 1 |
| 2 |
∴∠BOF=36°+27°=63°.
点评:本题考查了余角和角平分线的定义;弄清各个角之间的关系是解决问题的关键.

练习册系列答案
相关题目
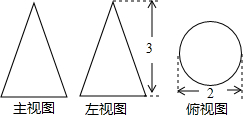 如图是某几何体的三视图,则对该几何体描述正确的是( )
如图是某几何体的三视图,则对该几何体描述正确的是( )| A、它是一个底面直径为2,高为3的圆柱 |
| B、它是一个底面积为π,高为3的圆锥 |
| C、它是一个底面积为4π,高为3的圆锥 |
| D、它是一个底面直径为3,高为2的圆柱 |
 如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=4cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<12),连接DE,当△BDE是直角三角形时,t的值为
如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=4cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<12),连接DE,当△BDE是直角三角形时,t的值为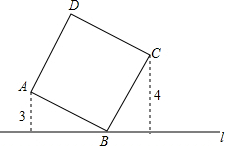 如图,直线l过正方形ABCD的顶点B,点A、点C到直线l的距离分别是3和4,则该正方形的边长是
如图,直线l过正方形ABCD的顶点B,点A、点C到直线l的距离分别是3和4,则该正方形的边长是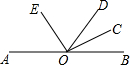 如图,AB是一条直线,OD是一条射线,OV,OE分别是∠BOD,∠AOD的平分线,∠BOC=15°48′.
如图,AB是一条直线,OD是一条射线,OV,OE分别是∠BOD,∠AOD的平分线,∠BOC=15°48′.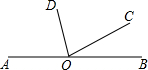 如图,∠BOC与∠AOC互为补角,OD平分∠AOC,∠BOC=n°,则∠DOB=
如图,∠BOC与∠AOC互为补角,OD平分∠AOC,∠BOC=n°,则∠DOB=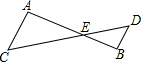 如图,已知△ACE∽△BDE,∠A=117°,∠C=37°,AC=6,BD=3,AB=12,CD=18,(1)求∠B和∠D的度数;
如图,已知△ACE∽△BDE,∠A=117°,∠C=37°,AC=6,BD=3,AB=12,CD=18,(1)求∠B和∠D的度数;