题目内容
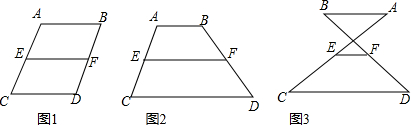
20.已知:AB∥CD∥EF,E为AC中点,AC∥BD,如图1所示,易证2EF=AB+CD(1)若AC与BD不平行,其它条件不变,如图2、图3,则在图2、图3两种情况下,线段EF,AB,CD又有怎样的数量关系?请直接写出你的猜想,并对其中一种情况给予证明;
(2)若∠C=∠D=60°,AB=3,EF=6,则AB与CD之间的距离为$\frac{3\sqrt{3}}{2}$.
分析 (1)作BH∥AC交CD于H,交EF于G,由已知得到2EG=AB+CH,根据三角形中位线定理得到GF=$\frac{1}{2}$DH,计算即可;
(2)作BR∥AC交CD于R,作BP⊥CD于P,根据平行四边形的性质得到CR=AB=3,求出RB,根据等边三角形的判定和性质解答即可.
解答 (1)如图2,2EF=AB+CD,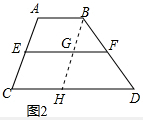
证明:作BH∥AC交CD于H,交EF于G,
由已知得,2EG=AB+CH,
∵AB∥CD∥EF,E为AC中点,
∴F是BD的中点,
∴GF是△BFD的中位线,
∴GF=$\frac{1}{2}$DH,
∴EF=EG+GF=$\frac{1}{2}$(AB+CH)+$\frac{1}{2}$DH,
∴2EF=AB+CD,
如图3,2EF=CD-AB;
(2)如图4,作BR∥AC交CD于R,作BP⊥CD于P,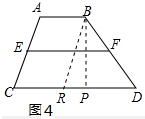
∴四边形ACRB是平行四边形,
∴CR=AB=3,
∴RD=CD-CR=3,
∵∠C=60°,BR∥AC,
∴∠BRD=∠C=60°,又∠D=60°,
∴△BRD是等边三角形,
∴BP=$\frac{3\sqrt{3}}{2}$,
∴AB与CD之间的距离为$\frac{3\sqrt{3}}{2}$.
故答案为:$\frac{3\sqrt{3}}{2}$.
点评 本题考查的是梯形的中位线定理、三角形的中位线定理和平行四边形的判定和性质,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
8. 如图,直线a∥b,∠1=50°,2=30°,则∠3的度数为( )
如图,直线a∥b,∠1=50°,2=30°,则∠3的度数为( )
 如图,直线a∥b,∠1=50°,2=30°,则∠3的度数为( )
如图,直线a∥b,∠1=50°,2=30°,则∠3的度数为( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
5. 如图,把一个30°的三角板和一个45°的三角板拼成如图所示的图案,则∠AEB=( )
如图,把一个30°的三角板和一个45°的三角板拼成如图所示的图案,则∠AEB=( )
 如图,把一个30°的三角板和一个45°的三角板拼成如图所示的图案,则∠AEB=( )
如图,把一个30°的三角板和一个45°的三角板拼成如图所示的图案,则∠AEB=( )| A. | 100° | B. | 55° | C. | 45° | D. | 75° |
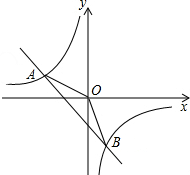 如图,一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$图象交于A(-2,1)、B(n,-2)两点.
如图,一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$图象交于A(-2,1)、B(n,-2)两点.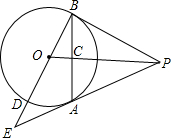 如图,PA为⊙O的切线,A为切点,过A作OP的垂线AB,垂足为点C,交⊙O于点B.延长BO与⊙O交于点B,延长BO与⊙O交于点D,与PA的延长线交于点E,
如图,PA为⊙O的切线,A为切点,过A作OP的垂线AB,垂足为点C,交⊙O于点B.延长BO与⊙O交于点B,延长BO与⊙O交于点D,与PA的延长线交于点E,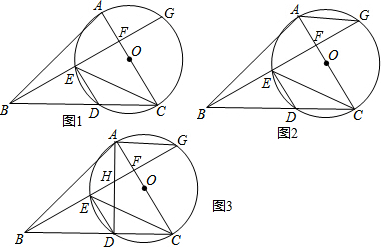
 如图,梯形的上底长为3x,下底长为5x-y,高为3x+2y,求这个梯形的面积.
如图,梯形的上底长为3x,下底长为5x-y,高为3x+2y,求这个梯形的面积.