题目内容
6.先化简,后求值:(1)($\frac{a}{a-b}$-$\frac{{a}^{2}}{{a}^{2}-2ab+{b}^{2}}$)÷($\frac{a}{a+b}$-$\frac{{a}^{2}}{{a}^{2}-{b}^{2}}$)+1,其中a=$\frac{2}{3}$,b=-3
(2)$({\frac{3x}{x-1}-\frac{x}{x+1}})•\frac{{{x^2}-1}}{x}$,其中x=2.
分析 (1)先根据分式混合运算的法则把原式进行化简,再把a,b的值代入进行计算即可;
(2)先根据分式混合运算的法则把原式进行化简,再把x的值代入进行计算即可.
解答 解:(1)原式=[$\frac{a}{a-b}$-$\frac{{a}^{2}}{(a-b)^{2}}$]÷[$\frac{a}{a+b}$-$\frac{{a}^{2}}{(a+b)(a-b)}$]+1
=$\frac{{a(a-b)-a}^{2}}{{(a-b)}^{2}}$÷$\frac{{a(a-b)-a}^{2}}{(a+b)(a-b)}$+1
=$\frac{-ab}{{(a-b)}^{2}}$•$\frac{(a+b)(a-b)}{-ab}$
=$\frac{a+b}{a-b}$,
当a=$\frac{2}{3}$,b=-3时,原式=$\frac{\frac{2}{3}-3}{\frac{2}{3}+3}$=-$\frac{7}{11}$;
(2)原式=$\frac{3x(x+1)-x(x-1)}{(x+1)(x-1)}$•$\frac{(x+1)(x-1)}{x}$
=$\frac{2{x}^{2}+4x}{(x+1)(x-1)}$•$\frac{(x+1)(x-1)}{x}$
=2x+4,
当x=2时,原式=4+4=8.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
1.从数轴上看,大于-3且小于2的整数有( )
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
18.为丰富学生学习生活,学校举行绘画展,小强所绘长为80cm,宽为50cm的图画被选中去参加展览,图画四周镶上一条等宽的金边装裱成一幅矩形挂图后,图画的面积是整个挂图面积的$\frac{20}{27}$.若设金边的宽度为xcm,那么x满足的方程是( )
| A. | $(80+2x)(50+2x)×\frac{20}{27}=80×50$ | B. | $(80+2x)(50+2x)=80×50×\frac{20}{27}$ | ||
| C. | $(80-2x)(50-2x)×\frac{20}{27}=80×50$ | D. | $(80-2x)(50-2x)=80×50×\frac{20}{27}$ |
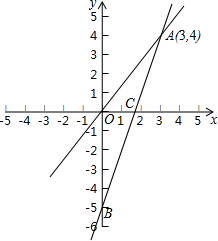 如图,一个正比例函数y1=k1x的图象与一个一次函数y2=k2x+b的图象相交于点A(3,4),且一次函数y2的图象与y轴相交于点B(0,-5),与x轴交于点C.
如图,一个正比例函数y1=k1x的图象与一个一次函数y2=k2x+b的图象相交于点A(3,4),且一次函数y2的图象与y轴相交于点B(0,-5),与x轴交于点C. 有理数在a,b,c在数轴上的位置如图所示,则|a+c|+|c-b|=-a-b.
有理数在a,b,c在数轴上的位置如图所示,则|a+c|+|c-b|=-a-b.