题目内容
14.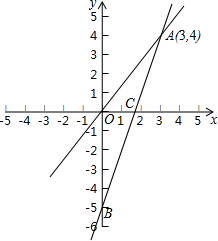 如图,一个正比例函数y1=k1x的图象与一个一次函数y2=k2x+b的图象相交于点A(3,4),且一次函数y2的图象与y轴相交于点B(0,-5),与x轴交于点C.
如图,一个正比例函数y1=k1x的图象与一个一次函数y2=k2x+b的图象相交于点A(3,4),且一次函数y2的图象与y轴相交于点B(0,-5),与x轴交于点C.(1)判断△AOB的形状并说明理由;
(2)若将直线AB绕点A旋转,使△AOC的面积为8,求旋转后直线AB的函数解析式;
(3)在x轴上求一点P使△POA为等腰三角形,请直接写出所有符合条件的点P的坐标.
分析 (1)根据坐标特征和勾股定理求出AO的长,根据等腰三角形的判定定理证明即可;
(2)根据三角形的面积公式求出OC的长,得到点C的坐标,利用待定系数法求出解析式即可;
(3)分OA=OP、OA=AP、OP=AP三种情况,结合图形、根据等腰三角形的性质、运用勾股定理解得即可.
解答 解:(1)∵点A的坐标为(3,4),
∴OA=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴OA=OB,
∴△AOB是等腰三角形;
(2)△AOC的面积=$\frac{1}{2}$×OC×4=8,
∴OC=4,
则点C的坐标为(4,0)或(-4,0),
当点C的坐标为(4,0)时,设旋转后直线AB的函数解析式为y=kx+b,
则$\left\{\begin{array}{l}{3k+b=4}\\{4k+b=0}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{k=-4}\\{b=16}\end{array}\right.$,
∴旋转后直线AB的函数解析式为y=-4x+16;
当点C的坐标为(-4,0)时,设旋转后直线AB的函数解析式为y=ax+c,
则$\left\{\begin{array}{l}{3a+c=4}\\{-4a+c=0}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{a=\frac{4}{7}}\\{b=\frac{16}{7}}\end{array}\right.$,
∴旋转后直线AB的函数解析式为y=$\frac{4}{7}$x+$\frac{16}{7}$,
答:旋转后直线AB的函数解析式为y=-4x+16或y=$\frac{4}{7}$x+$\frac{16}{7}$;
(3)当OA=OP时,点P的坐标为(-5,0)或(5,0),
当OA=AP时,∵点A的横坐标为3,
∴点P的坐标为(6,0),
当OP=AP时,
如图,设点P的坐标为(x,0),
则(x-3)2+42=x2,
解得,x=$\frac{25}{6}$,
∴点P的坐标为($\frac{25}{6}$,0),
∴所有符合条件的点P的坐标为:(-5,0);(5,0);(6,0);($\frac{25}{6}$,0).
点评 本题考查的是一次函数的应用、等腰三角形的性质、勾股定理,掌握待定系数法求一次函数解析式是解题的关键,注意分情况讨论思想、数形结合思想的应用.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 观察下图的规律,在“?”处填上的数字是( )
观察下图的规律,在“?”处填上的数字是( )| A. | 2 | B. | -2 | C. | 4 | D. | -4 |
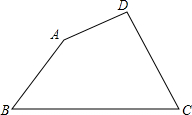 已知:四边形ABCD,∠B=50°,∠C=60°,满足AD+DC=BC,AB2+DC2=4AD2,求:∠A.
已知:四边形ABCD,∠B=50°,∠C=60°,满足AD+DC=BC,AB2+DC2=4AD2,求:∠A.