题目内容

17．抛物线y=-x2+2x+3与x轴交于A、B两点，则AB=4．

分析 根据抛物线与x轴的交点问题，通过解方程-x2+2x+3=0可得到点A和点B的坐标，然后利用两点间的距离公式可求出AB的长．

解答 解：当y=0时，-x2+2x+3=0，解得x1=-1，x2=3，
则A（-1，0），B（3，0），
所以AB=3-（-1）=4．
故答案为4．

点评 本题考查了抛物线与x轴的交点：把求二次函数y=ax2+bx+c（a，b，c是常数，a≠0）与x轴的交点坐标问题转化为解关于x的一元二次方程．

练习册系列答案
相关题目
9．计算：
（1）$\sqrt{32}$-2$\sqrt{\frac{1}{3}}$+$\sqrt{48}$-$\sqrt{\frac{1}{8}}$；
（2）（$\sqrt{8}$-2$\sqrt{0.25}$）-（$\sqrt{1\frac{1}{8}}$+$\sqrt{50}$+$\frac{2}{3}$$\sqrt{72}$）
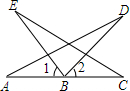8．如图，A、B、C在同一条直线上，∠1=∠2，AB=BC，BD=BE．求证：∠D=∠E．
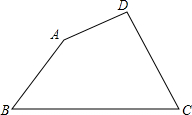5．已知：四边形ABCD，∠B=50°，∠C=60°，满足AD+DC=BC，AB2+DC2=4AD2，求：∠A．
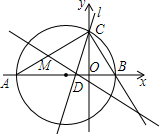12．在平面直角坐标系中，△ABC的边AB在x轴上，且OA＞OB，以AB为直径的圆与y轴正半轴交于点C，A、B两点的横坐标xA、xB是关于x的方程x2+3x-4=0的两个根．
（1）求点C的坐标；
（2）若∠ACB的平分线所在的直线l交x轴于点D，求直线l对应的一次函数关系式；
（3）过点D任作一直线l′分别交射线CA、CB（点C除外）于点M、N，则$\frac{1}{CM}$+$\frac{1}{CN}$的值是否为定值？若是，求出定值；若不是，请说明理由．
2．观察下图的规律，在“？”处填上的数字是（　　）
A．2B．-2C．4D．-4
9．抛物线y=-2（x+4）2-5的顶点坐标是（-4，-5）．
6．先化简，后求值：
（1）（$\frac{a}{a-b}$-$\frac{{a}^{2}}{{a}^{2}-2ab+{b}^{2}}$）÷（$\frac{a}{a+b}$-$\frac{{a}^{2}}{{a}^{2}-{b}^{2}}$）+1，其中a=$\frac{2}{3}$，b=-3
（2）$（{\frac{3x}{x-1}-\frac{x}{x+1}}）•\frac{{{x^2}-1}}{x}$，其中x=2．
7．如图为手的示意图，在各个手指间标记字母A、B、C、D．请你按图中箭头所指方向（即A→B→C→D→C→B→A→B→C→…的方式）从A开始 数连续的正整数1，2，3，4…，当数到12时，对应的字母是B；当字母C第201次出现时，恰好数到的数是603．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网