题目内容
12.如图1,B(-1,0),D(0,2),经过点C(3,0)的直线EC交直线BD于A,交y轴于E,使AD=AE(1)求证:AB=AC
(2)如图2,△ABC沿x轴方向平行移动时,AB交y轴于D,直线DF交AC延长线于F,交x轴于G且BD=CF,求证:OG长度不变.

分析 (1)根据等腰三角形的性质得到∠AED=∠ADE,由于∠ECO+∠AED=90°,∠DBO+∠BDO=90°,∠ADE=∠BDO,求得∠ECO=∠DBO,根据等腰三角形的判定即可得到结论;
(2)过F作FE⊥x轴于E,由(1)知∠1=∠2,等量代换得到1=∠3,推出△BOD≌△CEF,根据全等三角形的性质得到BO=CE,DO=EF,通过△DOG≌△FEG,得到OG=GE,于是得到OG=$\frac{1}{2}$OE,即可得到结论.
解答 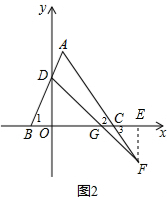 解:(1)∵AD=AE,
解:(1)∵AD=AE,
∴∠AED=∠ADE,
∵∠ECO+∠AED=90°,∠DBO+∠BDO=90°,∠ADE=∠BDO,
∴∠ECO=∠DBO,
∴AB=AC;
(2)过F作FE⊥x轴于E,由(1)知∠1=∠2,
∵∠2=∠3,
∴∠1=∠3,
在△BDO与△CEF中,
$\left\{\begin{array}{l}{∠1=∠3}\\{∠BOD=∠CEF}\\{BD=CF}\end{array}\right.$,
∴△BOD≌△CEF,
∴BO=CE,DO=EF,
在△DOG与△FEG中,
$\left\{\begin{array}{l}{∠DGO=∠FGE}\\{∠DOG=∠FEG}\\{DO=EF}\end{array}\right.$,
∴△DOG≌△FEG,
∴OG=GE,
∴OG=$\frac{1}{2}$OE,
∵BO=CE,
∴BO+OC=CE+OC,
即BC=OE,
∴OG=$\frac{1}{2}$OE=$\frac{1}{2}$BC=$\frac{1}{2}×4=2$,
即OG不变.
点评 本题考查了全等三角形的判定和性质,等腰三角形的性质,正确的作出辅助线构造全等三角形是解题的关键.

练习册系列答案
相关题目
17. 如图,在△ABC中,D为BC上一点,E为AD延长线上一点,BD:DC=5:3,∠C=∠E,若AD=4,BC=8,则DE的长为( )
如图,在△ABC中,D为BC上一点,E为AD延长线上一点,BD:DC=5:3,∠C=∠E,若AD=4,BC=8,则DE的长为( )
 如图,在△ABC中,D为BC上一点,E为AD延长线上一点,BD:DC=5:3,∠C=∠E,若AD=4,BC=8,则DE的长为( )
如图,在△ABC中,D为BC上一点,E为AD延长线上一点,BD:DC=5:3,∠C=∠E,若AD=4,BC=8,则DE的长为( )| A. | $\frac{15}{4}$ | B. | $\frac{15}{3}$ | C. | 5 | D. | 3 |

 如图,点O是等边△ABC内的一点.∠BOC=α,将△BOC绕点C按顺时针旋转60°得到△ADC,连接OD.
如图,点O是等边△ABC内的一点.∠BOC=α,将△BOC绕点C按顺时针旋转60°得到△ADC,连接OD. 如图,设正方体ABCD-A1B1C1D1的棱长为1,黑、白两个甲壳虫同时从点A出发,以相同的速度分别沿棱向前爬行,黑甲壳虫爬行的路线是AA1→A1D1→…,白甲壳虫爬行的路线是AB→BB1→…,并且都遵循如下规则:所爬行的第n+2与第n条棱所在的直线必须是既不平行也不相交(其中n是正整数),那么当黑、白两个甲壳虫各爬行完第2013条棱分别停止在所到的正方体顶点处时,它们之间的距离是$\sqrt{2}$.
如图,设正方体ABCD-A1B1C1D1的棱长为1,黑、白两个甲壳虫同时从点A出发,以相同的速度分别沿棱向前爬行,黑甲壳虫爬行的路线是AA1→A1D1→…,白甲壳虫爬行的路线是AB→BB1→…,并且都遵循如下规则:所爬行的第n+2与第n条棱所在的直线必须是既不平行也不相交(其中n是正整数),那么当黑、白两个甲壳虫各爬行完第2013条棱分别停止在所到的正方体顶点处时,它们之间的距离是$\sqrt{2}$.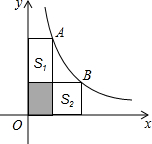 如图,A、B两点在双曲线$y=\frac{12}{x}$上,分别过A、B两点想坐标轴作垂线,若S阴影=3,则S1+S2的值为( )
如图,A、B两点在双曲线$y=\frac{12}{x}$上,分别过A、B两点想坐标轴作垂线,若S阴影=3,则S1+S2的值为( )
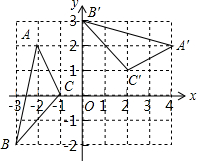 如图,在平面直角坐标系xOy中,△A′B′C′由△ABC绕点P旋转得到,则点P的坐标为(1,-1).
如图,在平面直角坐标系xOy中,△A′B′C′由△ABC绕点P旋转得到,则点P的坐标为(1,-1).