题目内容
1.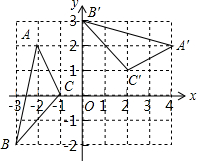 如图,在平面直角坐标系xOy中,△A′B′C′由△ABC绕点P旋转得到,则点P的坐标为(1,-1).
如图,在平面直角坐标系xOy中,△A′B′C′由△ABC绕点P旋转得到,则点P的坐标为(1,-1).
分析 连接AA′,CC′,线段AA′、CC′的垂直平分线的交点就是点P.
解答  解:连接AA′、CC′,
解:连接AA′、CC′,
作线段AA′的垂直平分线MN,作线段CC′的垂直平分线EF,
直线MN和直线EF的交点为P,点P就是旋转中心.
∵直线MN为:x=1,设直线CC′为y=kx+b,由题意:$\left\{\begin{array}{l}{-k+b=0}\\{2k+b=1}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=\frac{1}{3}}\\{b=\frac{1}{3}}\end{array}\right.$,
∴直线CC′为y=$\frac{1}{3}$x+$\frac{1}{3}$,
∵直线EF⊥CC′,经过CC′中点($\frac{1}{2}$,$\frac{1}{2}$),
∴直线EF为y=-3x+2,
由$\left\{\begin{array}{l}{x=1}\\{y=-3x+2}\end{array}\right.$得$\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$,
∴P(1,-1).
故答案为(1,-1).
点评 本题考查旋转的性质,掌握对应点连线段的垂直平分线的交点就是旋转中心,是解题的关键.

练习册系列答案
相关题目
 在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.请判断AE与CF的位置关系,并说明理由.
在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.请判断AE与CF的位置关系,并说明理由.
