题目内容
9.解方程:(1)x2-6x+8=0;
(2)x2-4x-3=0.
分析 (1)先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式(x-2)(x-4)=0,进而可得x-2=0,x-4=0,再解即可;
(2)首先确定a、b、c的值,然后可得△,再利用求根公式进行计算即可.
解答 解:(1)(x-2)(x-4)=0,
则x-2=0,x-4=0,
解得:x1=2,x2=4;
(2)x2-4x-3=0,
∵a=1,b=-4,c=-3,
∴△=b2-4ac=16+12=28,
∴x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{4±\sqrt{28}}{2}$=2$±\sqrt{7}$,
则x1=2+$\sqrt{7}$,x2=2-$\sqrt{7}$.
点评 此题主要考查了一元二次方程的解法,关键是掌握因式分解法和公式法解方程的步骤.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目
18. 连接边长为1的正方形对边中点,可将一个正方形分成四个全等的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成四个更小的小正方形,…重复这样的操作,则2016次操作后右下角的小正方形面积是( )
连接边长为1的正方形对边中点,可将一个正方形分成四个全等的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成四个更小的小正方形,…重复这样的操作,则2016次操作后右下角的小正方形面积是( )
 连接边长为1的正方形对边中点,可将一个正方形分成四个全等的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成四个更小的小正方形,…重复这样的操作,则2016次操作后右下角的小正方形面积是( )
连接边长为1的正方形对边中点,可将一个正方形分成四个全等的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成四个更小的小正方形,…重复这样的操作,则2016次操作后右下角的小正方形面积是( )| A. | $\frac{1}{2004}$ | B. | ${(\frac{1}{2})^{2016}}$ | C. | ${(\frac{1}{4})^{2016}}$ | D. | $1-{(\frac{1}{4})^{2016}}$ |

 将一个正方形纸片剪成如图中的四个小正方形,用同样的方法,每个小正方形又被剪成四个更小的正方形,这样连续5次后共得到16个小正方形.
将一个正方形纸片剪成如图中的四个小正方形,用同样的方法,每个小正方形又被剪成四个更小的正方形,这样连续5次后共得到16个小正方形.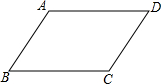 如图,AB=CD,AB∥DC.求证:AD∥BC,AD=BC.
如图,AB=CD,AB∥DC.求证:AD∥BC,AD=BC. 如图,在Rt△AOB中,∠AOB=90°,OA=OB=4,点C、D在边AB上,且∠COD=45°,设AD=x,BC=y.
如图,在Rt△AOB中,∠AOB=90°,OA=OB=4,点C、D在边AB上,且∠COD=45°,设AD=x,BC=y.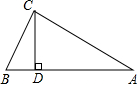 已知如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足是D,写出图中的一组相似三角形△ABC∽△ACD.
已知如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足是D,写出图中的一组相似三角形△ABC∽△ACD.