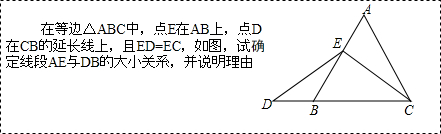
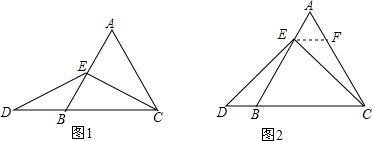
题目内容

1．解方程：
①x2-6x-4=0；       
②x2-12x+27=0．

分析 ①利用配方法解方程；
②利用因式分解法解方程．

解答 解：①x2-6x-4=0，
x2-6x=4，
x2-6x+9=4+9，
（x-3）2=13，
x-3=±$\sqrt{13}$，
所以x1=3+$\sqrt{13}$，x2=3-$\sqrt{13}$；
②（x-3）（x-9）=0，
x-3=0或x-9=0，
所以x1=3，x2=9．

点评 本题考查了解一元二次方程-因式分解法：就是先把方程的右边化为0，再把左边通过因式分解化为两个一次因式的积的形式，那么这两个因式的值就都有可能为0，这就能得到两个一元一次方程的解，这样也就把原方程进行了降次，把解一元二次方程转化为解一元一次方程的问题了（数学转化思想）．也考查了配方法解一元二次方程．

练习册系列答案
相关题目
20．阅读材料：
将一个直角三角形AOB（及其内部）绕其一条直角边AO所在直线旋转一周，所形成的几何体叫做圆锥．
圆锥的底面是以OB为半径的一个圆形．
圆锥的侧面展开是一个以A为圆心，斜边AB的长为半径的扇形，直角三角形AOB的斜边AB称为圆锥的一条母线，扇形的弧长就是圆锥底面的周长（如图所示）
圆锥表面积=S圆锥的侧面+S圆锥的底面
阅读后，请解答下面的问题：

从卡纸上剪下半径是30厘米（母线l=30厘米）的扇形，做一个圆锥纸盒，圆锥的底面圆O直径是20厘米（如图所示）
（1）求圆锥的底面圆O的周长；
（2）求剪下的扇形的圆心角；
（3）求圆锥的表面积．
12．已知：如图，AD平分∠BAC，DB⊥AB于B，DC⊥AC于C，求证：AB=AC．
9．解方程：
（1）x2-6x+8=0； 
（2）x2-4x-3=0．
16．把下列各数填入相应的大括号里
-0.78，5，+$\frac{1}{4}$，-0.87，-10，-$\frac{22}{7}$，0，$\frac{π}{3}$，0.$\stackrel{•}{3}\stackrel{•}{1}$，-2.121121112…
负整数：{-10…}
分数：{-0.78，+$\frac{1}{4}$，-0.87，-$\frac{22}{7}$，0.$\stackrel{•}{3}\stackrel{•}{1}$…}
非负数：{5，+$\frac{1}{4}$，0，$\frac{π}{3}$，0.$\stackrel{•}{3}\stackrel{•}{1}$…}
无理数：{$\frac{π}{3}$，-2.121121112…}…}．
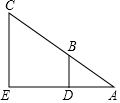6．如图，小东设计两个直角，来测量河宽DE，他量得AD=2m，BD=3m，CE=12m，则河宽DE=6m．
13．八年级数学课上，王老师出示了如下框中的题目．

小聪与同桌小明讨论后，进行了如下解答：
（1）特殊情况•探索结论
当点E为AB的中点时，如图1，确定线段AE与DB的大小关系．请你直接写出结论：AE=DB（填“＞”，“＜”或“=”）．

（2）特例启发•解答题目
解：如图2，题目中，AE与DB的大小关系是：AE=DB（填“＞”，“＜”或“=”）．
提示如下：过点E作EF∥BC，交AC于点F，（请你继续完成以下的解答过程）
（3）拓展结论•设计新题
在等边三角形ABC中，若点E在直线AB上，点D在直线CB上，且ED=EC．若△ABC的边长为2，AE=4，则CD=2或6．（请你直接写出结果）．
10．（1）若一次函数y=kx+b（k≠0）的图象经过点A（1，1）点B（2，3），求这个函数的解析式；
（2）若一直线与此一次函数的图象交于（-2，m）点，且与y轴的交点的坐标为（0，5），求这条直线的解析式．
11．若|a+3|=-（b-2）2，则ab的值为（　　）
A．-6B．-9C．9D．6

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网