题目内容
2.△ABC中,∠C=90°,AC=6,BC=8,E为射线BC上的一个动点,设BE=x(1)当点E在AB的垂直平分线上时,求x的值.
(2)当点C沿AE翻折后落在直线AB上时,求x的值.
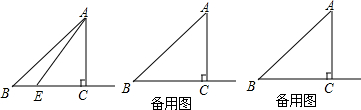
分析 (1)由线段垂直平分线的性质可知AE=BE=x,然后再在Rt△AEC中,依据勾股定理列方程求解即可;
(2)先由勾股定理求得AB=10,由翻折的性质求得BC′=4,C′E=8-x,在Rt△BEC′中,依据勾股定理列方程求解即可.
解答 解:(1)设BE=x,则EC=8-x.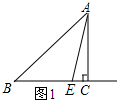
∵点E在AB的垂直平分线上,
∴AE=BE=x.
在Rt△AEC中,AE2=EC2+AC2,即x2=(8-x)2+62.
解得:x=$\frac{25}{4}$.
(2)如图2所示.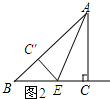
在Rt△ABC中,AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=10.
由翻折的性质可知:∠C=∠AC′E=90°,AC′=AC=6,EC=EC′.
在Rt△BEC′中,由勾股定理得:BE2=C′B2+C′E2,即x2=42+(8-x)2,
解得:x=5.
点评 本题主要考查的是翻折的性质、勾股定理、线段垂直平分线的性质,掌握翻折的性质、勾股定理、线段垂直平分线的性质是解题的关键.

练习册系列答案
相关题目
17.2015年宁波市前8个月新增贷款72000000000,用科学记数法表示为( )
| A. | 7.2×108 | B. | 7.2×109 | C. | 7.2×1010 | D. | 7.2×1011 |

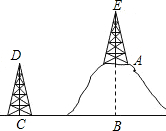 如图,小山高AB=75米,B,C两点间的水平距离为40米,两铁塔的高相等,即CD=AE.如果要在两铁塔顶D,E间架设一条高压线,那么这条高压线至少为多长?
如图,小山高AB=75米,B,C两点间的水平距离为40米,两铁塔的高相等,即CD=AE.如果要在两铁塔顶D,E间架设一条高压线,那么这条高压线至少为多长?