题目内容
10.点P(-2,-3)到原点的距离是$\sqrt{13}$.分析 作PA⊥x轴于A,连接OP,则∠OAP=90°,OA=2,PA=3,由勾股定理求出OP即可.
解答 解:作PA⊥x轴于A,连接OP,如图所示:
则∠OAP=90°,
∵P(-2,-3),
∴OA=2,PA=3,
由勾股定理得:OP=$\sqrt{O{A}^{2}+P{A}^{2}}$=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$,
即点P(-2,-3)到原点的距离是$\sqrt{13}$;
故答案为:$\sqrt{13}$.
点评 本题考查了勾股定理、坐标与图形性质;熟练掌握勾股定理,通过作辅助线运用勾股定理求出OP是解决问题的关键.

练习册系列答案
相关题目
5.两个不为零的有理数相除,如果交换被除数与除数的位置而商不变,那么这两个数一定是( )
| A. | 相等 | B. | 互为相反数 | ||
| C. | 互为倒数 | D. | 相等或互为相反数 |
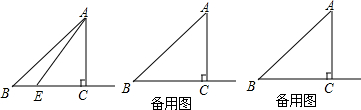
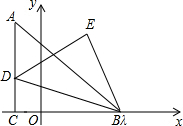 已知Rt△ABC中,∠ACB=90°,AC=BC,且点B(a+1,0),C(b,0)都在平面直角坐标系的x轴上,如图所示,且满足a2+b2-10a+4b+29=0,点D为射线AC上一动点且纵坐标为m,以BD为斜边,按顺时针顺序作△BDE,使∠DEB=90°,EB=ED.
已知Rt△ABC中,∠ACB=90°,AC=BC,且点B(a+1,0),C(b,0)都在平面直角坐标系的x轴上,如图所示,且满足a2+b2-10a+4b+29=0,点D为射线AC上一动点且纵坐标为m,以BD为斜边,按顺时针顺序作△BDE,使∠DEB=90°,EB=ED.