题目内容
如图，在梯形ABCD中，AD∥BC，△AOD的面积与△BOC的面积之比为1：9，△AOB的面积为6（1）AD：BC的值；
（2）梯形ABCD的面积．
考点：相似三角形的判定与性质,梯形
专题：
分析：（1）由平行可知△AOD∽△COB，利用面积比可求得相似比，可求得AD：BC；
（2）由条件可知S△ABD=S△ADC，可求得△COD的面积，再由条件可知S△AOB：S△AOD=BO：DO=BC：AD，可求得△AOD的面积，进一步可求得△BOC的面积，则可求得梯形ABCD的面积．
（2）由条件可知S△ABD=S△ADC，可求得△COD的面积，再由条件可知S△AOB：S△AOD=BO：DO=BC：AD，可求得△AOD的面积，进一步可求得△BOC的面积，则可求得梯形ABCD的面积．
解答：解：（1）∵AD∥BC，
∴△AOD∽△COB，
∴
=
=
=
，
即AD：BC=1：3；
（2）∵AD∥BC，
∴S△ABD=S△ADC，
∴S△COD=S△AOB=6，
又∵S△AOB：S△AOD=BO：DO=BC：AD=3：1，
∴S△AOD=2，
又∵S△AOD：S△BOC=1：9，
∴S△BOC=18，
∴S梯形ABCD=2+6+6+18=32．
∴△AOD∽△COB，
∴
| AD |
| BC |
|
|
| 1 |
| 3 |
即AD：BC=1：3；
（2）∵AD∥BC，
∴S△ABD=S△ADC，
∴S△COD=S△AOB=6，
又∵S△AOB：S△AOD=BO：DO=BC：AD=3：1，
∴S△AOD=2，
又∵S△AOD：S△BOC=1：9，
∴S△BOC=18，
∴S梯形ABCD=2+6+6+18=32．
点评：本题主要考查相似三角形的判定和性质，掌握相似三角形的面积比等于相似比是解题的关键．
练习册系列答案
相关题目
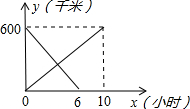一辆客车从甲地开往乙地，一辆出租车从乙地开往甲地，两车同时出发，两车距甲地的距离y千米与行驶时间x小时之间的函数图象如图所示，则下列说法中错误的是（ ）| A、客车比出租车晚4小时到达目的地 |
| B、客车速度为60千米/时，出租车速度为100千米/时 |
| C、两车出发后3.75小时相遇 |
| D、两车相遇时客车距乙地还有225千米 |
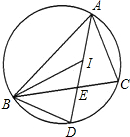如图，点I是△ABC的内心，线段AI的延长线交△ABC的外接圆于点D，交BC边于点E，求证：ID=BD．
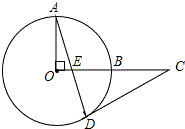如图，OA、OB是⊙O的半径，OA⊥OB，点C是OB延长线上一点，过点C作⊙O的切线，点D是切点，连接AD交OB于点E．求证：CD=CE．
如图，CD是⊙O的直径，CD=10，点A在⊙O上，∠ACD=30°，B为弧AD的中点，P是直径CD上一动点，则PA+PB的最小值为