题目内容
O是AB上一点,OC、OD是从O点引出的两条射线,OE平分∠AOC,∠BOC:∠AOE:∠AOD=2:5:8,求∠BOD的度数.
考点:角的计算
专题:
分析:结合题意画出图形,然后根据∠BOC:∠AOE:∠AOD=2:5:8,可以设∠BOC=2x,∠AOE=5x,∠AOD=8x,由OE平分∠AOC,得∠AOC=2∠AOE=10x,由∠AOC+∠BOC=180°,可解x的值,进而求出∠AOD的度数,由∠AOD+∠BOD=180°,可求∠BOD的度数.
解答:解:结合题意画出图形

∵∠BOC:∠AOE:∠AOD=2:5:8,
∴可以设∠BOC=2x,∠AOE=5x,∠AOD=8x,
∵OE平分∠AOC,
∴∠AOC=2∠AOE=10x,
∵∠AOC+∠BOC=180°,
∴10x+2x=180°,
解得:x=15°,
∴∠AOD=8x=120°,
∵∠AOD+∠BOD=180°,
∴∠BOD=180°-∠AOD=180°-120°=60°.

∵∠BOC:∠AOE:∠AOD=2:5:8,
∴可以设∠BOC=2x,∠AOE=5x,∠AOD=8x,
∵OE平分∠AOC,
∴∠AOC=2∠AOE=10x,
∵∠AOC+∠BOC=180°,
∴10x+2x=180°,
解得:x=15°,
∴∠AOD=8x=120°,
∵∠AOD+∠BOD=180°,
∴∠BOD=180°-∠AOD=180°-120°=60°.
点评:此题考查了角的计算,解题的关键是:结合题意画出图形,然后根据∠BOC:∠AOE:∠AOD=2:5:8,可以设∠BOC=2x,∠AOE=5x,∠AOD=8x,然后根据邻补角互补即可求出角的度数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
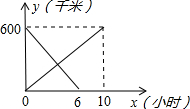 一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,两车距甲地的距离y千米与行驶时间x小时之间的函数图象如图所示,则下列说法中错误的是( )
一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,两车距甲地的距离y千米与行驶时间x小时之间的函数图象如图所示,则下列说法中错误的是( )| A、客车比出租车晚4小时到达目的地 |
| B、客车速度为60千米/时,出租车速度为100千米/时 |
| C、两车出发后3.75小时相遇 |
| D、两车相遇时客车距乙地还有225千米 |
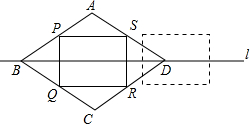 在菱形ABCD中,AB=5cm,BD=8cm,P,Q,R,S分别是菱形各边的中点.将长方形PQRS沿着直线L向右移动5cm,则长方形PQRS与菱形ABCD重叠的面积是多少?
在菱形ABCD中,AB=5cm,BD=8cm,P,Q,R,S分别是菱形各边的中点.将长方形PQRS沿着直线L向右移动5cm,则长方形PQRS与菱形ABCD重叠的面积是多少? 已知线段a、b(a>b)
已知线段a、b(a>b)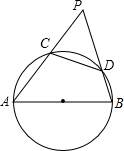 如图,已知圆的直径,AB=6cm,CD是圆上长为2cm的弦,当弦CD在半圆AB上滑动时,AC和BD延长线的夹角是否为定值?如果不是,说明理由;如果是,求出这个定角的正弦值.
如图,已知圆的直径,AB=6cm,CD是圆上长为2cm的弦,当弦CD在半圆AB上滑动时,AC和BD延长线的夹角是否为定值?如果不是,说明理由;如果是,求出这个定角的正弦值.