题目内容
 如图所示,正五边形ABCDE的对角线AC和BE相交于点M,求证;
如图所示,正五边形ABCDE的对角线AC和BE相交于点M,求证;(1)AC∥DE;
(2)ME=AE.
考点:正多边形和圆
专题:证明题
分析:(1)根据正多边形求出∠ABC=∠EAB=∠DCB=∠DEA=
=108°,AB=BC,求出∠CAB=∠BCA=36°,求出∠EAC=72°,最后求出∠DEA+∠EAC=180°即可;
(2)求出∠EAM=∠EMA=72°,即可得出答案.
| (5-2)×180° |
| 5 |
(2)求出∠EAM=∠EMA=72°,即可得出答案.
解答:证明:(1)∵五边形ABCDE是正五边形,
∴∠ABC=∠EAB=∠DCB=∠DEA=
=108°,AB=BC,
∴∠CAB=∠BCA=36°,
∴∠EAC=108°-36°=72°,
∴∠DEA+∠EAC=108°+72°=180°,
∴AC∥DE;
(2)∵五边形ABCDE是正五边形,
∴∠ABC=∠EAB=∠DCB=∠DEA=
=108°,AE=AB,
∴∠AEB=∠ABE=36°,
∵∠EAC=72°,
∴∠EMA=180°-36°-72°=72°,
∴∠EAM=∠EMA,
∴ME=AE.
∴∠ABC=∠EAB=∠DCB=∠DEA=
| (5-2)×180° |
| 5 |
∴∠CAB=∠BCA=36°,
∴∠EAC=108°-36°=72°,
∴∠DEA+∠EAC=108°+72°=180°,
∴AC∥DE;

(2)∵五边形ABCDE是正五边形,
∴∠ABC=∠EAB=∠DCB=∠DEA=
| (5-2)×180° |
| 5 |
∴∠AEB=∠ABE=36°,
∵∠EAC=72°,
∴∠EMA=180°-36°-72°=72°,
∴∠EAM=∠EMA,
∴ME=AE.
点评:本题考查了正多边形的性质,等腰三角形的性质,平行线的判定的应用,解此题的关键是能求出各个角的度数.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
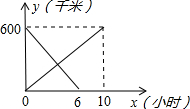 一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,两车距甲地的距离y千米与行驶时间x小时之间的函数图象如图所示,则下列说法中错误的是( )
一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,两车距甲地的距离y千米与行驶时间x小时之间的函数图象如图所示,则下列说法中错误的是( )| A、客车比出租车晚4小时到达目的地 |
| B、客车速度为60千米/时,出租车速度为100千米/时 |
| C、两车出发后3.75小时相遇 |
| D、两车相遇时客车距乙地还有225千米 |
“六一”期间,某商店将单价标为130元的书包按8折出售可获利30%,该书包每个的进价是( )
| A、65元 | B、80元 |
| C、100元 | D、104元 |
 已知线段a、b(a>b)
已知线段a、b(a>b)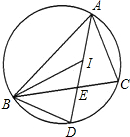 如图,点I是△ABC的内心,线段AI的延长线交△ABC的外接圆于点D,交BC边于点E,求证:ID=BD.
如图,点I是△ABC的内心,线段AI的延长线交△ABC的外接圆于点D,交BC边于点E,求证:ID=BD.