题目内容
9．已知：$\frac{x}{2}$=$\frac{y}{3}$=$\frac{z}{4}$，求$\frac{2x+3y-4z}{x+y+z}$的值．分析 直接利用已知用同一未知数表示出x，y，z的值，进而代入化简即可．
解答 解：∵$\frac{x}{2}$=$\frac{y}{3}$=$\frac{z}{4}$，
∴设x=2a，则y=3a，z=4a，
∴$\frac{2x+3y-4z}{x+y+z}$=$\frac{4a+9a-16a}{2a+3a+4a}$=-$\frac{1}{3}$．
点评 此题主要考查了比例的性质，正确用一个未知数表示出各数是解题关键．
练习册系列答案
相关题目
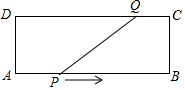如图，在矩形ABCD中，AB=16cm，AD=6cm，动点P，Q分别从点A，C同时出发，点P以每秒3cm的速度向点B移动，点Q以每秒12cm测得速度向点D移动，当点P到达点B处时，两点均停止移动
如图，AD=BC=BA，那么∠1与∠2之间的关系是2∠1+∠2=180°．
17．已知△ABC中，tanA=$\frac{1}{2}$，下列说法正确的是（ ）
| A． | tanB=2 | B． | tanB=$\frac{1}{2}$ | C． | sinA=$\frac{2\sqrt{5}}{5}$ | D． | sinA=$\frac{\sqrt{5}}{5}$ |
如图，点C、B、E在同一条直线上，AB∥DE，∠ACB=∠CDE，AC=CD，求证：AB=CE．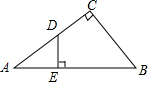
在△ABC中，∠ACB=90°，DE⊥AB．
如图所示，有一根直立标杆，它的上部被风从B处吹折，杆顶C着地离杆底2米，修好后又被风吹折，因新断处D比前一次低0.5米，故杆顶E着地比前一次远1米，求原标杆的长度？