Question

19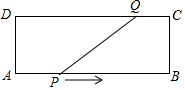．如图，在矩形ABCD中，AB=16cm，AD=6cm，动点P，Q分别从点A，C同时出发，点P以每秒3cm的速度向点B移动，点Q以每秒12cm测得速度向点D移动，当点P到达点B处时，两点均停止移动
（1）P，Q两点出发多长时间，线段PQ的长度为10cm？
（2）是否存在某一时刻，使四边形PBCQ为正方形？若存在，求出该时刻；若不存在，请说明理由．

Answer 1

分析 （1）过点P作PH⊥CD，利用勾股定理解答即可；
（2）利用正方形的性质进行解答即可．

解答 解：（1）过点P作PH⊥CD于点H，
∴HQ=16-5t，
∴PQ²=PH²+HQ²，
即10²=（16-5t）²+6²，
解得：${t}_{1}=\frac{8}{5}，{t}_{2}=\frac{24}{5}$（舍去），
答：P，Q两点出发$\frac{8}{5}$秒，线段PQ的长度为10cm；
（2）∵四边形PBCQ是正方形，
∴BP=CQ，即16-3t=2t，
解得：t=$\frac{16}{5}$，
∵$CQ=2t=\frac{32}{5}≠6$，
∴不成立．

点评 此题考查正方形的性质，关键是根据利用正方形的性质进行解答．