题目内容
15.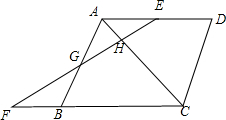 如图,在菱形ABCD中,E是AD的中点,EF⊥AC,交AB于G,交CB延长线于F.求证:GE=GF.
如图,在菱形ABCD中,E是AD的中点,EF⊥AC,交AB于G,交CB延长线于F.求证:GE=GF.
分析 首先连接BD,由在菱形ABCD中,EF⊥AC,可证得四边形EFBD是平行四边形,又由E是AD的中点,根据三角形中位线的性质,可证得GE=$\frac{1}{2}$BD,继而证得结论.
解答  证明:连接BD,
证明:连接BD,
∵四边形ABCD是菱形,
∴AD∥BC,BD⊥AC,
∵EF⊥AC,
∴EF∥BD,
∴四边形EFBD是平行四边形,
∴EF=BD,
∵E是AD的中点,
∴GE=$\frac{1}{2}$BD,
∴GE=$\frac{1}{2}$EF,
∴GE=GF.
点评 此题考查了菱形的性质、平行四边形的判定与性质以及三角形中位线的性质.注意准确作出辅助线是解此题的关键.

练习册系列答案
相关题目
3. 如图,在Rt△ABC中,∠C=90°,ED是AB的垂直平分线,交AC于点D,交AB于E,已知∠CBD=10°,则∠A的度数为( )
如图,在Rt△ABC中,∠C=90°,ED是AB的垂直平分线,交AC于点D,交AB于E,已知∠CBD=10°,则∠A的度数为( )
 如图,在Rt△ABC中,∠C=90°,ED是AB的垂直平分线,交AC于点D,交AB于E,已知∠CBD=10°,则∠A的度数为( )
如图,在Rt△ABC中,∠C=90°,ED是AB的垂直平分线,交AC于点D,交AB于E,已知∠CBD=10°,则∠A的度数为( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
7.计算(3.5×103)×(2.2×105)的结果并用科学记数法表示,正确的结果是( )
| A. | 770000000 | B. | 77×107 | C. | 7.7×108 | D. | 7.7×107 |
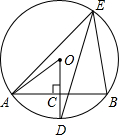 如图,AB是⊙O的一条弦,点D是弧AB的中点,OD交AB于点C,点E在⊙O上. 若∠OAC=40°,求∠DEB的度数.
如图,AB是⊙O的一条弦,点D是弧AB的中点,OD交AB于点C,点E在⊙O上. 若∠OAC=40°,求∠DEB的度数. 如图,六边形ABCDEF中,AF=CD,AB=DE,FE=BC,∠B=∠E,求证:AF∥CD.
如图,六边形ABCDEF中,AF=CD,AB=DE,FE=BC,∠B=∠E,求证:AF∥CD.