题目内容
已知抛物线y=x2-7x+10与x轴的交于A、B两点(A在B点左侧),抛物线上一点P的横坐标为4,则在抛物线AP段(不包括A、P点)上是否存在一点M,使得△MAP的面积最大?若存在,求出这个最大值及此时M点的坐标;若不存在,请说明理由.
考点:抛物线与x轴的交点
专题:计算题
分析:作MH⊥x轴于H,交AP于N,先解方程x2-7x+10=0确定A点坐标为(2,0),B点坐标为(5,0),再确定P点坐标为(4,-2),然后利用待定系数法确定为直线AP的解析式为y=-x+2,设M点坐标为(x,x2-7x+10),则N点坐标为(x,-x+2),则MN=-x2+6x-8,接着得到S△APM=S△MNA+S△MNP=
•(4-2)•(-x2+6x-8),于是可根据二次的最值问题进行求解.
| 1 |
| 2 |
解答:解:存在.
如图,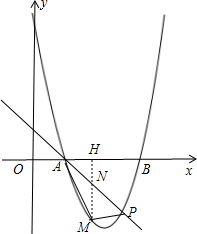 作MH⊥x轴于H,交AP于N,
作MH⊥x轴于H,交AP于N,
把y=0代入y=x2-7x+10得x2-7x+10=0,解得x1=2,x2=5,
∴A点坐标为(2,0),B点坐标为(5,0),
把x=4代入y=x2-7x+10得y=16-28+10=-2,
∴P点坐标为(4,-2),
设直线AP的解析式为y=kx+b,
把A(2,0)、P(4,-2)代入得
,解得
,
∴直线AP的解析式为y=-x+2,
设M点坐标为(x,x2-7x+10),则N点坐标为(x,-x+2),
∴MN=-x+2-(x2-7x+10)=-x2+6x-8,
∴S△APM=S△MNA+S△MNP=
•(4-2)•(-x2+6x-8)=-x2+6x-8=-(x-3)2+1,
∴当x=3时,△MAP的面积最大值为1,
把x=3代入y=x2-7x+10得y=9-21+10=-2,
∴此时M点坐标为(3,-2).
如图,
 作MH⊥x轴于H,交AP于N,
作MH⊥x轴于H,交AP于N,把y=0代入y=x2-7x+10得x2-7x+10=0,解得x1=2,x2=5,
∴A点坐标为(2,0),B点坐标为(5,0),
把x=4代入y=x2-7x+10得y=16-28+10=-2,
∴P点坐标为(4,-2),
设直线AP的解析式为y=kx+b,
把A(2,0)、P(4,-2)代入得
|
|
∴直线AP的解析式为y=-x+2,
设M点坐标为(x,x2-7x+10),则N点坐标为(x,-x+2),
∴MN=-x+2-(x2-7x+10)=-x2+6x-8,
∴S△APM=S△MNA+S△MNP=
| 1 |
| 2 |
∴当x=3时,△MAP的面积最大值为1,
把x=3代入y=x2-7x+10得y=9-21+10=-2,
∴此时M点坐标为(3,-2).
点评:本题考查了抛物线与x轴的交点:求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的交点与一元二次方程ax2+bx+c=0根之间的关系,△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
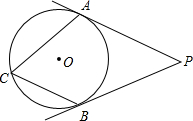 如图,PA,PB是⊙O的切线,切点分别为A,B,且∠APB=50°,点C是优弧AB上的一点.
如图,PA,PB是⊙O的切线,切点分别为A,B,且∠APB=50°,点C是优弧AB上的一点.
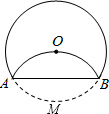 如图,将⊙O沿AB折叠后,圆弧恰好经过圆心,求
如图,将⊙O沿AB折叠后,圆弧恰好经过圆心,求 如图,A,B,C,D四张卡片上分别写有-2,
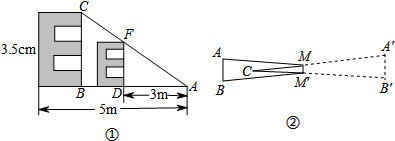
如图,A,B,C,D四张卡片上分别写有-2,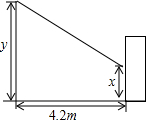 我们知道,在同一时刻的物高与影长成比例.某兴趣小组利用这一知识进行实地测量,其中有一部分同学在某时刻测得竖立在地面上的一根长为1m的竹竿的影长是1.4m,另一部分同学在同一时刻对树影进行测量(如图),可惜树太靠近一幢建筑物(相距4.2m),树影不完全落在地面上,有一部分树影落在建筑物的墙壁上.
我们知道,在同一时刻的物高与影长成比例.某兴趣小组利用这一知识进行实地测量,其中有一部分同学在某时刻测得竖立在地面上的一根长为1m的竹竿的影长是1.4m,另一部分同学在同一时刻对树影进行测量(如图),可惜树太靠近一幢建筑物(相距4.2m),树影不完全落在地面上,有一部分树影落在建筑物的墙壁上. 某开发区的大标语牌上,要画出如图中阴影部分的三种标点符号:“句号”,“逗号”和“问号”.已知小圆半径为r,大圆半径为2r,若用油漆均匀涂刷一遍,问哪一个标点符号用的油漆最多?哪一个标点符号用的油漆最少?
某开发区的大标语牌上,要画出如图中阴影部分的三种标点符号:“句号”,“逗号”和“问号”.已知小圆半径为r,大圆半径为2r,若用油漆均匀涂刷一遍,问哪一个标点符号用的油漆最多?哪一个标点符号用的油漆最少?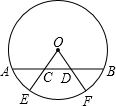 如图,在⊙O中,E,F为
如图,在⊙O中,E,F为