题目内容
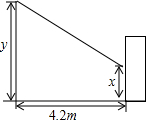 我们知道,在同一时刻的物高与影长成比例.某兴趣小组利用这一知识进行实地测量,其中有一部分同学在某时刻测得竖立在地面上的一根长为1m的竹竿的影长是1.4m,另一部分同学在同一时刻对树影进行测量(如图),可惜树太靠近一幢建筑物(相距4.2m),树影不完全落在地面上,有一部分树影落在建筑物的墙壁上.
我们知道,在同一时刻的物高与影长成比例.某兴趣小组利用这一知识进行实地测量,其中有一部分同学在某时刻测得竖立在地面上的一根长为1m的竹竿的影长是1.4m,另一部分同学在同一时刻对树影进行测量(如图),可惜树太靠近一幢建筑物(相距4.2m),树影不完全落在地面上,有一部分树影落在建筑物的墙壁上.(1)若设树高为y(m),树在墙壁上的影长为x(m),请你给出计算树高的表达式;
(2)若树高5m,则此时留在墙壁上的树影有多高?
考点:相似三角形的应用,平行投影
专题:
分析:(1)利用同一时刻的物高与影长成比例,进而得出y与x的关系式;
(2)利用(1)中所求得出x的值即可.
(2)利用(1)中所求得出x的值即可.
解答: 解:(1)过点E作EB⊥AC于点B,
解:(1)过点E作EB⊥AC于点B,
由题意可得出:
=
,
∴
=
;
∴树高的表达式为:y=3+x;
(2)若树高5m,则此时留在墙壁上的树影有:5=3+x,
解得:x=2.
答:此时留在墙壁上的树影有2m.
 解:(1)过点E作EB⊥AC于点B,
解:(1)过点E作EB⊥AC于点B,由题意可得出:
| AB |
| BE |
| 1 |
| 1.4 |
∴
| y-x |
| 4.2 |
| 1 |
| 1.4 |
∴树高的表达式为:y=3+x;
(2)若树高5m,则此时留在墙壁上的树影有:5=3+x,
解得:x=2.
答:此时留在墙壁上的树影有2m.
点评:此题主要考查了相似三角的应用,利用同一时刻的物高与影长成比例得出是解题关键.

练习册系列答案
相关题目
 把图①按一定比例缩小为图②(图②中的一条线段是图①长方形按比例缩小后的长),请你把图②补画完整.
把图①按一定比例缩小为图②(图②中的一条线段是图①长方形按比例缩小后的长),请你把图②补画完整.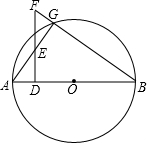 如图,AB是⊙O的直径,FB交⊙O于点G,FD⊥AB,垂足为D,FD交AG于点E.求证:EF•DE=AE•EG.
如图,AB是⊙O的直径,FB交⊙O于点G,FD⊥AB,垂足为D,FD交AG于点E.求证:EF•DE=AE•EG.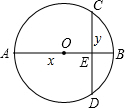 善于归纳和总结的小明发现,“数形结合”是初中数学的基本思想方法,被广泛地应用在数学学习和解决问题中.用数量关系描述图形性质和用图形性质描述数量关系,往往会有新的发现.小明在研究垂直于直径的弦的性质过程中(如图,直径AB⊥弦CD于点E,设AE=x,BE=y,用含x,y的式子表示图中的弦CD的长度),通过比较运动的弦CD和与之垂直的直径AB的大小关系,发现了一个关于正数x,y的不等式,你也能发现这个不等式吗?写出你发现的不等式.
善于归纳和总结的小明发现,“数形结合”是初中数学的基本思想方法,被广泛地应用在数学学习和解决问题中.用数量关系描述图形性质和用图形性质描述数量关系,往往会有新的发现.小明在研究垂直于直径的弦的性质过程中(如图,直径AB⊥弦CD于点E,设AE=x,BE=y,用含x,y的式子表示图中的弦CD的长度),通过比较运动的弦CD和与之垂直的直径AB的大小关系,发现了一个关于正数x,y的不等式,你也能发现这个不等式吗?写出你发现的不等式.