题目内容
为了加强视力保护意识,欢欢想在书房里挂一张测试距离为5m的视力表,但两面墙的距离只有3m.在一次课题学习课上,欢欢向全班同学征集“解决空间过小,如何放置视力表问题”的方案,其中甲、乙两位同学设计方案新颖,构思巧妙.
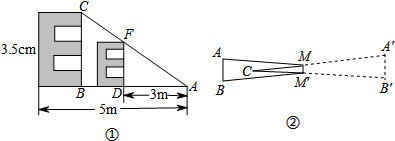
(1)甲生的方案:如图①,根据测试距离为5m的大视力表制作一个测试距离为3m的小视力表.如果大视力表中“E”的高是3.5cm,那么小视力表中相应“E”的高是多少?
(2)乙生的方案:使用平面镜来解决房间小的问题.如图②,若使墙面镜子能呈现完整的视力表,由平面镜成像原理,作出了光路图,其中视力表AB的上、下边沿A,B发出的光线经平面镜MM′的上下边沿反射后射人人眼C处.如果视力表的全长为0.8m,请计算出镜长至少为多少米.

(1)甲生的方案:如图①,根据测试距离为5m的大视力表制作一个测试距离为3m的小视力表.如果大视力表中“E”的高是3.5cm,那么小视力表中相应“E”的高是多少?
(2)乙生的方案:使用平面镜来解决房间小的问题.如图②,若使墙面镜子能呈现完整的视力表,由平面镜成像原理,作出了光路图,其中视力表AB的上、下边沿A,B发出的光线经平面镜MM′的上下边沿反射后射人人眼C处.如果视力表的全长为0.8m,请计算出镜长至少为多少米.
考点:相似三角形的应用
专题:
分析:(1)先根据题意得出△ADF∽△ABC,再由相似三角形的对应边成比例即可得出结论;
(2)作CD⊥MM′,垂足为D,并延长交A′B′于E,根据平行线的性质可知CE⊥A′B′,由相似三角形的判定定理可得出△CMM′∽△CA′B′,再根据相似三角形的对应边成比例即可得出结论.
(2)作CD⊥MM′,垂足为D,并延长交A′B′于E,根据平行线的性质可知CE⊥A′B′,由相似三角形的判定定理可得出△CMM′∽△CA′B′,再根据相似三角形的对应边成比例即可得出结论.
解答:解:(1)∵FD∥BC
∴△ADF∽△ABC.
∴
=
.
∴
=
.
∴FD=2.1(cm).
答:小视力表中相应“E”的长是2.1cm;
(2)解:作CD⊥MM′,垂足为D,并延长交A′B′于E,
∵AB∥MM′∥A′B′,
∴CE⊥A′B′,
∴△CMM′∽△CA′B′,
∴
=
,
又∵CD=CE-DE=5-3=2,CE=5,A′B′=AB=0.8,
∴
=
,
∴MM′=0.32(米),
∴镜长至少为0.32米.
∴△ADF∽△ABC.
∴
| FD |
| BC |
| AD |
| AB |
∴
| FD |
| 3.5 |
| 3 |
| 5 |
∴FD=2.1(cm).
答:小视力表中相应“E”的长是2.1cm;
(2)解:作CD⊥MM′,垂足为D,并延长交A′B′于E,
∵AB∥MM′∥A′B′,
∴CE⊥A′B′,
∴△CMM′∽△CA′B′,
∴
| MM′ |
| A′B′ |
| CD |
| CE |
又∵CD=CE-DE=5-3=2,CE=5,A′B′=AB=0.8,
∴
| MM′ |
| 0.8 |
| 2 |
| 5 |
∴MM′=0.32(米),
∴镜长至少为0.32米.
点评:本题考查的是相似三角形的应用,根据题意作出辅助线,构造出相似三角形是解答此题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目

 如图,移动其中两根火柴棒,使图形变成一个中心对称图形.
如图,移动其中两根火柴棒,使图形变成一个中心对称图形.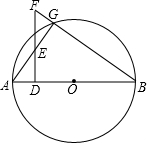 如图,AB是⊙O的直径,FB交⊙O于点G,FD⊥AB,垂足为D,FD交AG于点E.求证:EF•DE=AE•EG.
如图,AB是⊙O的直径,FB交⊙O于点G,FD⊥AB,垂足为D,FD交AG于点E.求证:EF•DE=AE•EG.