题目内容
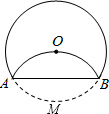 如图,将⊙O沿AB折叠后,圆弧恰好经过圆心,求
如图,将⊙O沿AB折叠后,圆弧恰好经过圆心,求 |
| AMB |
考点:垂径定理,含30度角的直角三角形,翻折变换(折叠问题)
专题:计算题
分析:连接OA,OM,OB,由折叠的性质得到ON=MN,都为半径的一半,在直角三角形AON中,利用直角边等于斜边的一半确定出∠OAB=30°,同理得到∠OBA=30°,确定出∠AOB=120°,即可得出弧AMB的度数.
解答: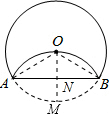 解:连接OA,OM,OB,
解:连接OA,OM,OB,
由折叠得到ON=MN=
OM,且OM⊥AB,即N为AB的中点,
在Rt△AON中,ON=
OA,
∴∠OAB=30°,
同理∠OBA=30°,
∴∠AOB=120°,
则
的度数为120°.
 解:连接OA,OM,OB,
解:连接OA,OM,OB,由折叠得到ON=MN=
| 1 |
| 2 |
在Rt△AON中,ON=
| 1 |
| 2 |
∴∠OAB=30°,
同理∠OBA=30°,
∴∠AOB=120°,
则
 |
| AMB |
点评:此题考查了垂径定理,翻折变换,以及含30度角的直角三角形,熟练掌握垂径定理是解本题的关键.

练习册系列答案
相关题目
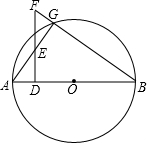 如图,AB是⊙O的直径,FB交⊙O于点G,FD⊥AB,垂足为D,FD交AG于点E.求证:EF•DE=AE•EG.
如图,AB是⊙O的直径,FB交⊙O于点G,FD⊥AB,垂足为D,FD交AG于点E.求证:EF•DE=AE•EG.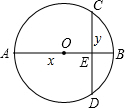 善于归纳和总结的小明发现,“数形结合”是初中数学的基本思想方法,被广泛地应用在数学学习和解决问题中.用数量关系描述图形性质和用图形性质描述数量关系,往往会有新的发现.小明在研究垂直于直径的弦的性质过程中(如图,直径AB⊥弦CD于点E,设AE=x,BE=y,用含x,y的式子表示图中的弦CD的长度),通过比较运动的弦CD和与之垂直的直径AB的大小关系,发现了一个关于正数x,y的不等式,你也能发现这个不等式吗?写出你发现的不等式.
善于归纳和总结的小明发现,“数形结合”是初中数学的基本思想方法,被广泛地应用在数学学习和解决问题中.用数量关系描述图形性质和用图形性质描述数量关系,往往会有新的发现.小明在研究垂直于直径的弦的性质过程中(如图,直径AB⊥弦CD于点E,设AE=x,BE=y,用含x,y的式子表示图中的弦CD的长度),通过比较运动的弦CD和与之垂直的直径AB的大小关系,发现了一个关于正数x,y的不等式,你也能发现这个不等式吗?写出你发现的不等式. 如图,在Rt△ABC中,∠C=90°.
如图,在Rt△ABC中,∠C=90°.