题目内容
因式分【解析】
x2﹣3x =______________.
x(x-3)
【解析】试题分析：提取公因式x即可，即x2﹣3x=x（x﹣3）．
练习册系列答案
相关题目
已知等腰△ABC中，AB=AC，D是BC边上一点，连接AD，若△ACD和△ABD都是等腰三角形，则∠C的度数是 ．
36°或45°．
【解析】
试题分析：△ACD和△ABD都是等腰三角形，但没有说具体的边相等，所以应分情况讨论．
（1）AD=BD，DC=AD，那么△ADB和△ADC是全等三角形，可求得∠ADC=90°，那么∠C=45°；
（2）AB=BD，CD=AD，那么∠B=∠C=∠DAC，∠BAD=∠BDA=2∠C，然后用∠C表示出△ABC的内角和，即可求得5∠C=180°，那么∠C... 如图，拦水坝的横断面为等腰梯形ABCD，坝顶宽BC为6 m，坝高为3.2 m，为了提高水坝的拦水能力需要将水坝加高2 m，并且保持坝顶宽度不变，迎水坡CD的坡度不变，但是背水坡的坡度由原来的1∶2变成1∶2.5(坡度是坡高与坡的水平长度的比)．求加高后的坝底HD的长为多少．
29.4 m.
【解析】试题分析：应把所求的HD进行合理分割=HN+NF+FD，可利用Rt△MHN和Rt△EFD中的三角函数来做．
试题解析：由题意得BG＝3.2 m，MN＝EF＝3.2＋2＝5.2(m)，ME＝NF＝BC＝6 m，
在Rt△DEF中，∵，
∴FD＝2EF＝2×5.2＝10.4(m)，
在Rt△HMN中，∵，
∴HN＝2.5MN＝13(m)，
... 为了测量被池塘隔开的A，B两点之间的距离，根据实际情况，作出如图所示的图形，其中AB⊥BE，EF⊥BE，AF交BE于点D，C在BD上．有四位同学分别测量出以下4组数据：①BC，∠ACB；②CD，∠ACB，∠ADB；③EF，DE，BD；④DE，DC，BC.能根据所测数据，求出A，B两点之间距离的有( )
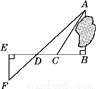
A. 1组 B. 2组 C. 3组 D. 4组
C
【解析】试题分析：此题比较综合，要多方面考虑，
①因为知道∠ACB和BC的长，所以可利用∠ACB的正切来求AB的长；
②可利用∠ACB和∠ADB的正切求出AB；
③因为△ABD∽△EFD可利用，求出AB；
④无法求出A，B间距离．
故共有3组可以求出A，B间距离．
故选C． 分解因式：2ab2－6a2b＋ab;
ab(2b－6a＋1)
【解析】试题分析：根据提公因式法分解因式，先确定公因式ab，再提取公因式即可.
试题解析：2ab2－6a2b＋ab = ab(2b－6a＋1). 把a2﹣4a多项式分解因式，结果正确的是（ ）
A. a（a﹣4） B. （a+2）（a﹣2） C. a（a+2）（a﹣2） D. （a﹣2）2﹣4
A
【解析】试题分析： a2-4a=a（a-4），
故选A． 如图所示，将Rt△ABC沿直角边AB的方向向右平移2个单位得到△DEF，如果AB＝4，∠ABC＝90°，且△ABC的面积为6，试求图中阴影部分的面积．
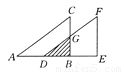
【解析】试题分析：根据△ABC的面积求出BC的长，根据平移的性质计算出BD的长，再根据平行线分线段成比例定理求出BG的长，最后利用三角形的面积公式计算即可得出答案．
试题解析：
【解析】
因为S△ABC＝AB·BC＝6，
所以BC＝3，
由平移可知AD＝2，BC∥EF，
所以BD＝AB－AD＝4－2＝2，
所以＝，
所以BG＝BC＝，
所以S△BD... 如图，在Rt△ABC中，AC⊥BC，CD⊥AB，∠1=∠2，有下列结论：（1）AC∥DE；（2）∠A=∠3；（3）∠B=∠1；（4）∠B与∠2互余；（5）∠A=∠2．其中正确的有 （填写所有正确的序号）．
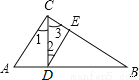
(1)、(2)、(3)
【解析】
试题分析：根据∠1=∠2，即内错角相等，两直线平行可得AC∥DE，则①正确；根据∠1+∠3=∠1+∠A=90°可得∠3=∠A，则②正确；根据∠1+∠3=∠3+∠B=90°可得∠B=∠1，则③正确；根据平行可得DE⊥BC，则∠3+∠2=∠B+∠3=90°，则∠2=∠B，则④错误；根据∠1=∠2，∠1≠∠A可得∠2≠∠A，则⑤错误. 平移前后两个图形__________
全等
【解析】试题解析：图形平移前后两个图形是全等的.
故答案为：全等.