题目内容
如图所示，将Rt△ABC沿直角边AB的方向向右平移2个单位得到△DEF，如果AB＝4，∠ABC＝90°，且△ABC的面积为6，试求图中阴影部分的面积．
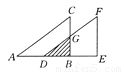
【解析】试题分析：根据△ABC的面积求出BC的长，根据平移的性质计算出BD的长，再根据平行线分线段成比例定理求出BG的长，最后利用三角形的面积公式计算即可得出答案．
试题解析：
【解析】
因为S△ABC＝AB·BC＝6，
所以BC＝3，
由平移可知AD＝2，BC∥EF，
所以BD＝AB－AD＝4－2＝2，
所以＝，
所以BG＝BC＝，
所以S△BD...
练习册系列答案
相关题目
作线段AB和CD，且AB和CD互相垂直平分，交点为O，AB＝2CD．分别取OA、OB、OC、OD的中点A′、B′、C′、D′，连结CA′、DA′、CB′、DB′、AC′、AD′、BC′、BD′得到一个四角星图案．将此四角星沿水平方向向右平移2厘米，作出平移前后的图形．
见解析
【解析】试题分析：根据垂直平分线的意义，画线段AB（4厘米），作AB的垂直平分线段CD（2厘米）交AB于点O，再分别取OA、OB、OC、OD的中点A′、B′、C′、D′，连结CA′、DA′、CB′、DB′、AC′、AD′、BC′、BD′得到一个四角形图案A′B′C′D′；再根据平移图形的特征，把四角形图案A′B′C′D′的四个顶点分别向右平移2厘米，再首尾连结各点，即可得到四角形图案... 如图，在某监测点B处望见一艘正在作业的渔船在南偏西15°方向的A处，若渔船沿北偏西75°方向以40海里/小时的速度航行，航行半小时后到达C处，在C处观测到B在C的北偏东60°方向上，则B、C之间的距离为（ ）
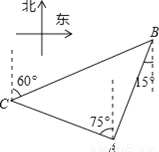
A. 20海里 B.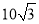 
海里 C. 20
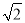海里 D. 30海里
C
【解析】∵∠ABE＝15°，AD∥BE，
∴∠DAB＝∠ABE＝15°，
∴∠CAB＝∠CAD＋∠DAB＝90°．
∵∠FCB＝60°，CF∥BE，
∴∠CBE＝∠FCB＝60°．
又∠CBA＋∠ABE＝∠CBE，
∴∠CBA＝45°．
在Rt△ABC中，
，
解得海里．
故选C． 因式分【解析】
x2﹣3x =______________.
x(x-3)
【解析】试题分析：提取公因式x即可，即x2﹣3x=x（x﹣3）． A，B两点间有一条传输速度为每分钟5米的传送带，由A点向B点传送货物．一只蚂蚁不小心爬到了传送带上，它以每分钟1.5米的速度从A点爬向B点，3分钟后，蚂蚁爬到了B点，你能求出A，B两点间的距离吗?
19.5米．
【解析】试题分析：蚂蚁的爬行速度是1.5米/分，传送带的传送速度为5米/分，并且传送带的传送方向与蚂蚁的爬行方向相同，所以蚂蚁从A点向B运动的速度是(5＋1.5)米/分，运动的时间是3分，根据路程＝速度×时间即可得出A，B两点间的距离．
试题解析：
【解析】
蚂蚁运动的速度是5＋1.5＝6.5米/分，
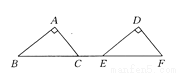
所以A，B两点间的距离是：6.5×3＝19.5米． 如图所示，△ABC经过平移得到△DEF，已知CE＝2 cm，AC＝3 cm，AB＝4 cm，∠A＝90°，则CF＝_________cm，平移的距离是_________．
7 7 cm
【解析】试题分析：在Rt△ABC中，由勾股定理得：
BC＝＝＝5（cm），
∵△ABC经过平移得到△DEF，
∴EF＝BC＝5cm，
∴CF＝CE＋EF＝2＋5＝7（cm），
∵C点与F点对应，
∴平移的距离是CF的长度，
即平移的距离是7cm．
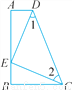
故答案为：7，7cm． 如图，∠A＝∠B＝90°，E是AB上一点，且AE＝BC，∠1＝∠2.求证：△ADE≌△BEC.
证明见解析
【解析】试题分析：由∠1=∠2，可得DE=CD，根据证明直角三角形全等的“HL”定理，证明即可.
试题解析：∵∠1＝∠2，
∴DE＝EC.
又∵∠A＝∠B＝90°，AE＝BC，
∴Rt△ADE≌Rt△BEC(HL). 下列可使两个直角三角形全等的条件是（ ）
A. 一条边对应相等 B. 两条直角边对应相等
C. 一个锐角对应相等 D. 两个锐角对应相等
B
【解析】【解析】
两直角三角形隐含一个条件是两直角相等，要判定两直角三角形全等，起码还要两个条件，故可排除A、C；
而D构成了AAA，不能判定全等；
B构成了SAS，可以判定两个直角三角形全等．
故选B． 将长度为5cm的线段向上平移10cm所得线段长度是（ ）
A. 10cm B. 5cm C. 0cm D. 无法确定
B
【解析】平移不改变图形的大小和形状．故线段长度不变，仍为5cm．