题目内容
7.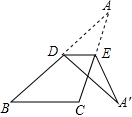 如图,在△ABC中,D,E分别是边AB,AC的中点,∠B=30°.现将△ADE沿DE折叠,点A落在三角形所在平面内的点为A′,则∠BDA′的度数为( )
如图,在△ABC中,D,E分别是边AB,AC的中点,∠B=30°.现将△ADE沿DE折叠,点A落在三角形所在平面内的点为A′,则∠BDA′的度数为( )| A. | 100° | B. | 120° | C. | 130° | D. | 140° |
分析 由三角形的中位线定理可知DE∥BC,从而可得到∠ADE=∠B=30°,然后由翻折的性质可知:∠EDA′=∠EDA=30°,最后根据∠BDA′=180°-∠EDA′-∠EDA求解即可.
解答 解:∵D,E分别是边AB,AC的中点,
∴DE∥BC.
∴∠ADE=∠B=30°.
由翻折的性质可知:∠EDA′=∠EDA=30°,
∠BDA′=180°-∠EDA′-∠EDA=180°-30°-30°=120°.
故选:B.
点评 本题主要考查的是三角形中位线定理和翻折变换,求得∠EDA′=∠EDA=30°是解题的关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
18.9的算术平方根是( )
| A. | ±3 | B. | ±$\sqrt{9}$ | C. | 3 | D. | -3 |
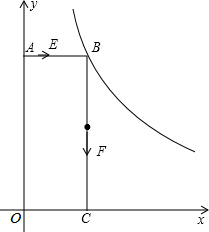 如图,已知:矩形AOCB的顶点B在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,且AB=3,BC=8.
如图,已知:矩形AOCB的顶点B在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,且AB=3,BC=8.