题目内容
15.如图1,在平面直角坐标系中,抛物线y=-$\frac{1}{4}$x2+bx+c经过点S(0,6)和点T(8,6),ST的垂直平分线交抛物线于点B.交x轴交于点C,以BC为直径作⊙P,交y轴于点A,M(点A在点M的下方).(1)求该抛物线的解析式;
(2)求出点A的坐标;
(3)如图2,在射线AB上有一动点D,在直线BC上有一动点E,若△ACD的重心为F,且以点A,F,D,E为顶点的四边形是平行四边形,求AF的长.
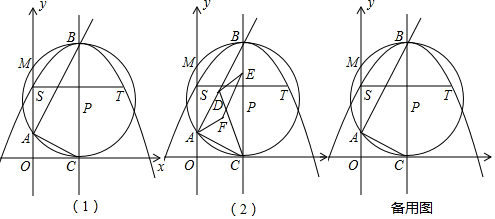
分析 (1)把S(0,6)和点T(8,6)的坐标代入y=-$\frac{1}{4}$x2+bx+c,转化为解方程组即可.
(2)如图1中,作AH⊥BC于H,则四边形OAHC是矩形,OA=HC,AH=OC.首先证明点B是抛物线的顶点,B(4,10),C(4,0),设OA=HC=x,再证明△AHC∽△BHC,可得AH2=CH•BH,即16=x(10-x),解方程即可解决问题.
(3)如图2中,延长AF交CD于N,连接AE、CD.首先求出直线AB的解析式为y=2x+2,设D(m,2m+2),由F是△ADC的内心,推出点N是CD的中点,推出N(m+2,m+1),推出AF=2FN,推出点F的横坐标为$\frac{2}{3}$(m+2),因为四边形ADEN是平行四边形,所以线段DF的中点的横坐标与线段AE的中点的横坐标相同,都是2,可得$\frac{m+\frac{2}{3}(m+2)}{2}$=2,解得m=$\frac{8}{5}$,再想办法求出点F的坐标即可解决问题.
解答 解:(1)把S(0,6)和点T(8,6)的坐标代入y=-$\frac{1}{4}$x2+bx+c得到$\left\{\begin{array}{l}{c=6}\\{-16+8b+c=6}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=2}\\{c=2}\end{array}\right.$,
∴抛物线的解析式为y=-$\frac{1}{4}$x2+2x+6,.
(2)如图1中,作AH⊥BC于H,则四边形OAHC是矩形,OA=HC,AH=OC.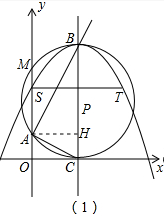
∵S、T关于对称轴x=4对称,BC垂直平分线段ST,
∴点B是抛物线的顶点,B(4,10),C(4,0),设OA=HC=x
∵BC是直径,
∴∠BAC=∠AHB=90°,
∴∠CAH+∠BAH=90°,∠BAH+∠ABH=90°,
∴∠CAH=∠ABH,∵∠AHC=∠AHB=90°,
∴△AHC∽△BHC,
∴AH2=CH•BH,
∴16=x(10-x),
解得x=2或8(舍弃),
∴点A坐标(0,2).
(3)如图2中,延长AF交CD于N,连接AE、CD.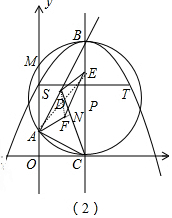
∵A(0,2),B(4,10),
∴直线AB的解析式为y=2x+2,设D(m,2m+2),
∵F是△ADC的重心,
∴点N是CD的中点,
∴N(m+2,m+1),
∵AF=2FN,
∴点F的横坐标为$\frac{2}{3}$(m+2),
∵四边形ADEN是平行四边形,
∴线段DF的中点的横坐标与线段AE的中点的横坐标相同,都是2,
∴$\frac{m+\frac{2}{3}(m+2)}{2}$=2,
解得m=$\frac{8}{5}$,
∴D($\frac{8}{5}$,$\frac{26}{5}$),N($\frac{18}{5}$,$\frac{13}{5}$),
∴直线AN的解析式为y=$\frac{1}{6}$x+2,
∴F($\frac{12}{5}$,$\frac{12}{5}$),
∴AF=$\sqrt{(\frac{12}{5})^{2}+(\frac{12}{5}-2)^{2}}$=$\frac{2\sqrt{37}}{5}$.
点评 本题考查二次函数综合题、一次函数的应用、相似三角形的判定和性质、勾股定理、三角形的重心、中点坐标公式等知识,解题的关键是灵活运用所学知识解决问题,学会利用此时想办法构建方程解决问题,属于中考压轴题.

 全能练考卷系列答案
全能练考卷系列答案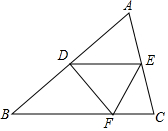 如图,点D、E分别是边AB、AC的中点,将△ADE沿着DE对折,点A落在BC边上的点F,若∠B=50°,则∠BDF的度数为( )
如图,点D、E分别是边AB、AC的中点,将△ADE沿着DE对折,点A落在BC边上的点F,若∠B=50°,则∠BDF的度数为( )| A. | 50° | B. | 70° | C. | 75° | D. | 80° |
 如图,在△ABC中,中线BE,CD相交于点O,连接DE,则下列判断错误的是( )
如图,在△ABC中,中线BE,CD相交于点O,连接DE,则下列判断错误的是( )| A. | DE是△ABC的中位线 | B. | 点O是△ABC的重心 | ||
| C. | △DEO∽△CBO | D. | $\frac{{S}_{△DOE}}{{S}_{△ADE}}$=$\frac{1}{2}$ |
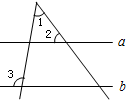 如图,直线a∥b,若∠1=50°,∠3=95°,则∠2的度数为( )
如图,直线a∥b,若∠1=50°,∠3=95°,则∠2的度数为( )| A. | 35° | B. | 40° | C. | 45° | D. | 55° |
 如图,已知△ABC与△BDE都是等边三角形,点D在边AC上(不与A、C重合),DE与AB相交于点F,则图中有( )对相似三角形(全等除外)
如图,已知△ABC与△BDE都是等边三角形,点D在边AC上(不与A、C重合),DE与AB相交于点F,则图中有( )对相似三角形(全等除外)