题目内容
5.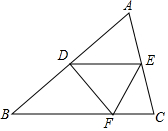 如图,点D、E分别是边AB、AC的中点,将△ADE沿着DE对折,点A落在BC边上的点F,若∠B=50°,则∠BDF的度数为( )
如图,点D、E分别是边AB、AC的中点,将△ADE沿着DE对折,点A落在BC边上的点F,若∠B=50°,则∠BDF的度数为( )| A. | 50° | B. | 70° | C. | 75° | D. | 80° |
分析 先根据点D、E分别边AB、AC的中点可知DE是△ABC的中位线,故可求出∠ADE=∠B=50°,再由翻折变换的性质可知∠EDF=50°,由平角的性质即可求解.
解答 解:∵点D、E分别边AB、AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,
∴∠ADE=∠B=50°,
∵△DEF是△DEA经过翻折变换得到的,
∴∠EDF=50°,
∴∠BDF=180°-2∠ADE=180°-100°=80°.
故选:D.
点评 本题考查的是图形翻折变换的性质及平角的性质,熟知折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等的知识是解答此题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
16.若x-y>x,且x+y<y,则下列不等式中正确的是( )
| A. | xy<0 | B. | $\frac{x}{y}$>0 | C. | x+y>0 | D. | x-y<0 |
13.在四边形ABCD中,AB∥CD,当满足什么条件时,四边形ABCD是平行四边形( )
| A. | ∠A+∠B=180° | B. | ∠B+∠D=180° | C. | ∠B+∠C=180° | D. | ∠A+∠B=180° |
20. 如图,OA⊥OC,OB⊥OD,四位同学分别说了自己的观点.甲:∠AOB=∠COD,乙:∠BOC+∠AOD=180°,丙:∠AOB与∠COD都是∠BOC的余角,丁:图中小于平角的角有4个,其中正确的结论有( )
如图,OA⊥OC,OB⊥OD,四位同学分别说了自己的观点.甲:∠AOB=∠COD,乙:∠BOC+∠AOD=180°,丙:∠AOB与∠COD都是∠BOC的余角,丁:图中小于平角的角有4个,其中正确的结论有( )
 如图,OA⊥OC,OB⊥OD,四位同学分别说了自己的观点.甲:∠AOB=∠COD,乙:∠BOC+∠AOD=180°,丙:∠AOB与∠COD都是∠BOC的余角,丁:图中小于平角的角有4个,其中正确的结论有( )
如图,OA⊥OC,OB⊥OD,四位同学分别说了自己的观点.甲:∠AOB=∠COD,乙:∠BOC+∠AOD=180°,丙:∠AOB与∠COD都是∠BOC的余角,丁:图中小于平角的角有4个,其中正确的结论有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.下列计算正确的是( )
| A. | (a+b)(b-a)=a2-b2 | B. | (a-b)2=a2-b2 | ||
| C. | (2x-y)2=4x2-2xy+y2 | D. | (x-2y)(-2y-x)=4y2-x2 |
14.半径为6的圆中,120°的圆心角所对的弧长是( )
| A. | 4π | B. | 5π | C. | 6π | D. | 8π |
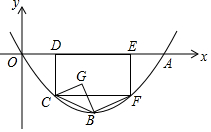 如图,在平面直角坐标系中,抛物线y=$\frac{1}{2}$ax2-2ax(a>0)与x轴正半轴交于点A,点B是抛物线的顶点,矩形CDEF的顶点D、E在x正半轴上,C、F在抛物线上,且点D的横坐标为1,连结BC、BF,以BC为斜边向右侧作等腰直角三角形BCG
如图,在平面直角坐标系中,抛物线y=$\frac{1}{2}$ax2-2ax(a>0)与x轴正半轴交于点A,点B是抛物线的顶点,矩形CDEF的顶点D、E在x正半轴上,C、F在抛物线上,且点D的横坐标为1,连结BC、BF,以BC为斜边向右侧作等腰直角三角形BCG