题目内容
14.一组按规律排列的式子:$\frac{a}{2}$,$\frac{{a}^{3}}{4}$,$\frac{{a}^{5}}{6}$,$\frac{{a}^{7}}{8}$,…则第n个式子是$\frac{{a}^{2n-1}}{2n}$(n为正整数).分析 观察分子、分母的变化规律,总结出一般规律即可.
解答 解:a,a3,a5,a7…,分子可表示为:a2n-1,
2,4,6,8,…分母可表示为2n,
则第n个式子为:$\frac{{a}^{2n-1}}{2n}$,
故答案为:$\frac{{a}^{2n-1}}{2n}$.
点评 本题考查了单项式的知识,属于基础题,关键是观察分子、分母的变化规律.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.与方程组$\left\{\begin{array}{l}{x+3y=-3}\\{x+y=-2}\end{array}\right.$有相同解的方程组是( )
| A. | $\left\{\begin{array}{l}{x-y=1}\\{3x=5-y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=y-1}\\{3x=5-y}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=y-1}\\{3x+5+y=0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=y-1}\\{3x+5-y=0}\end{array}\right.$ |
9.南京青奥会的成功举办,赢得了国际奥委会的高度赞扬,也促使了中国与世界各国青年的交流与沟通,据不完全统计,在青奥会举办期间,共有来自世界各地的约33.8万青年人相聚南京,33.8万用科学记数法表示为( )
| A. | 33.8×104 | B. | 3.38×104 | C. | 3.38×105 | D. | 0.338×106 |

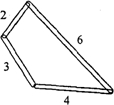 如图,用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依次为2、3、4、6,且相邻两木条的夹角均可调整.若调整木条的夹角时不破坏此木框,则任意两个螺丝间的距离的最大值为( )
如图,用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依次为2、3、4、6,且相邻两木条的夹角均可调整.若调整木条的夹角时不破坏此木框,则任意两个螺丝间的距离的最大值为( )