题目内容
如图，在△ABC中，AC=4，BC=6，D是AB的中点．（1）作出△CDB关于点D的中心对称图形．
（2）求出CD的取值范围．
考点：作图-旋转变换,三角形三边关系
专题：
分析：（1）利用旋转图形的性质得出延长CD到E，使DE=DC，进而得出符合题意的图形；
（2）根据三角形三边关系得出EC的取值范围，进而得出DC的取值范围．
（2）根据三角形三边关系得出EC的取值范围，进而得出DC的取值范围．
解答：
解：（1）延长CD到E，使DE=DC，连接AE，则△ADE即是所求的三角形；
（2）由对称性知，AE=BC=6，根据三角形三边关系得出：
6-4＜CE＜6+4，
即2＜EC＜10，
∴1＜CD＜5．
解：（1）延长CD到E，使DE=DC，连接AE，则△ADE即是所求的三角形；（2）由对称性知，AE=BC=6，根据三角形三边关系得出：
6-4＜CE＜6+4，
即2＜EC＜10，
∴1＜CD＜5．
点评：此题主要考查了三角形三边关系以及旋转变换图形，利用中心对称图形的性质得出是解题关键．
练习册系列答案
相关题目
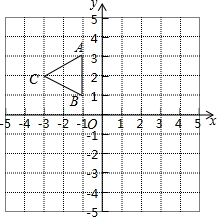如图，△ABC三个顶点坐标分别为A（-1，3），B（-1，1），C（-3，2），以原点O为位似中心，将△ABC放大为原来的2倍得到△A1B1C1，请在第四象限内画出△A1B1C1，并写出A1、B1、C1三点的坐标．
已知等腰三角形周长为40．
如图，一艘轮船在A处看见巡逻艇M在其北偏东58°的方向上，此时一艘客船在B处看见巡逻艇M在其北偏东12°的方向上，则此时从巡逻艇上看这两艘船的视角∠AMB=