题目内容
18. 如图,直线AB、CD相交于点O,OE⊥AB,O为垂足,如果∠DOB是∠EOD的两倍,即∠DOB=2∠EOD,求∠AOC,∠COB的度数.
如图,直线AB、CD相交于点O,OE⊥AB,O为垂足,如果∠DOB是∠EOD的两倍,即∠DOB=2∠EOD,求∠AOC,∠COB的度数.
分析 由垂直得∠EOB=90°,即∠EOD与∠DOB互余;再根据已知∠DOB是∠EOD的两倍,得∠DOB=60°,由对顶角相等和邻补角性质得出结论.
解答 解:∵OE⊥AB,
∴∠EOB=90°,
∴∠EOD+∠DOB=90°,
∵∠DOB=2∠EOD,
∴∠DOB=60°,
∴∠AOC=∠DOB=60°,
∴∠COB=180°-60°=120°.
点评 本题考查了垂线的定义及对顶角和邻补角性质,要注意∠DOB是∠EOD的两倍和垂线的定义的结合运用,得方程组或比的关系,可求这两个角的度数.

练习册系列答案
相关题目
8.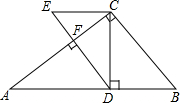 如图,在Rt△ACB中,∠ACB=90°,CD⊥AB于D,DF⊥AC于F,过C作CE∥AB交DF的延长线于点E,则下列结论中错误的是( )
如图,在Rt△ACB中,∠ACB=90°,CD⊥AB于D,DF⊥AC于F,过C作CE∥AB交DF的延长线于点E,则下列结论中错误的是( )
 如图,在Rt△ACB中,∠ACB=90°,CD⊥AB于D,DF⊥AC于F,过C作CE∥AB交DF的延长线于点E,则下列结论中错误的是( )
如图,在Rt△ACB中,∠ACB=90°,CD⊥AB于D,DF⊥AC于F,过C作CE∥AB交DF的延长线于点E,则下列结论中错误的是( )| A. | DE2=BD•AB | B. | S△CEF:S△ADF=BD2:AD2 | ||
| C. | $\frac{BD}{CA}$=$\frac{CF}{AD}$ | D. | $\frac{DF}{BC}$=$\frac{AF}{AB}$ |
10.若a>b,则下列各式中正确的是( )
| A. | a-$\frac{1}{5}$<b-$\frac{1}{5}$ | B. | -4a>-4b | C. | -2a+1<-2b+1 | D. | a2>b2 |
8.下列调查中,适合全面调查的是( )
| A. | 长江某段水域的水污染情况的调查 | B. | 你校数学教师的年龄状况的调查 | ||
| C. | 各厂家生产的电池使用寿命的调查 | D. | 我市居民环保意识的调查 |