题目内容
9.从数-2,-1,1,2,4中任取两个,其和的绝对值为k(k是自然数)的概率记作Pk.(如:P3是任取两个数,其和的绝对值为3的概率)(1)求k的所有取值;
(2)求P3;
(3)能否找到概率Pi,Pj,Pm,Pn(i<j<m<n ),使得Pi+Pj+Pm+Pn=0.7?若能找到,请举例说明;若不能找到,请说明理由.
分析 (1)从五个数中任取两个,得出所有的可能,求出两数之和的绝对值,即可确定出k的值;
(2)找出任取两个数,其和的绝对值为3的情况数,求出所求的概率即可;
(3)能找到,举一个例子即可.
解答 解:(1)从数-2,-1,1,2,4中任取两个,所有情况有10种,分别为:(-2,-1);(-2,1);(-2,2);(-2,4);(-1,1);(-1,2);(-1,4);(1,2);(1,4);(2,4),其和的绝对值为0,1,2,3,5,6,
则k=0,1,2,3,5,6;
(2)和的绝对值为3的情况有3种,
则P3=$\frac{3}{10}$;
(3)能找到概率Pi,Pj,Pm,Pn,使得Pi+Pj+Pm+Pn=0.7,
例如:P0=$\frac{1}{5}$,P1=$\frac{1}{5}$,P2=$\frac{1}{10}$,P3=$\frac{3}{10}$,P5=$\frac{1}{10}$,P6=$\frac{1}{10}$,使得P1+P2+P3+P5=0.7(答案不唯一).
点评 此题考查了列表法与树状图法,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
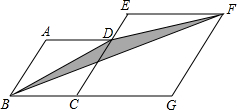 如图,菱形ABCD和菱形ECGF的边长分别为2和4,∠A=120°.则阴影部分面积是$\sqrt{3}$.(结果保留根号)
如图,菱形ABCD和菱形ECGF的边长分别为2和4,∠A=120°.则阴影部分面积是$\sqrt{3}$.(结果保留根号)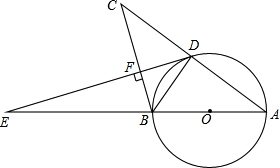 如图,在△ABC中,以AB为直径的⊙O与AC交于D点,过点D作DF⊥BC交AB的延长线于点E,垂足为F,∠FDB=∠A.
如图,在△ABC中,以AB为直径的⊙O与AC交于D点,过点D作DF⊥BC交AB的延长线于点E,垂足为F,∠FDB=∠A.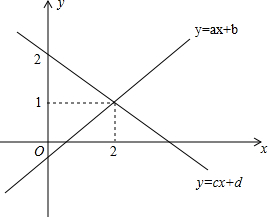 如图,直线y=ax+b与直线y=cx+d相交于点(2,1),则关于x的一元一次方程ax+b=cx+d的解为x=2.
如图,直线y=ax+b与直线y=cx+d相交于点(2,1),则关于x的一元一次方程ax+b=cx+d的解为x=2.