题目内容
1.已知线段AB=1,C为线段AB的黄金分割点,且AC>BC,求AC-BC的值.分析 根据黄金分割的定义先计算出AC=$\frac{\sqrt{5}-1}{2}$AB=$\frac{\sqrt{5}-1}{2}$,再利用BC=AB-AC计算出BC,然后计算AC-BC.
解答 解:∵C为线段AB的黄金分割点,且AC>BC,
∴AC=$\frac{\sqrt{5}-1}{2}$AB=$\frac{\sqrt{5}-1}{2}$,
∴BC=AB-AC=1-$\frac{\sqrt{5}-1}{2}$=$\frac{3-\sqrt{5}}{2}$,
∴AC-BC=$\frac{\sqrt{5}-1}{2}$-$\frac{3-\sqrt{5}}{2}$=$\sqrt{5}$-2
点评 本题考查了黄金分割:把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项(即AB:AC=AC:BC),叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点.其中AC=$\frac{\sqrt{5}-1}{2}$AB≈0.618AB,并且线段AB的黄金分割点有两个.

练习册系列答案
相关题目
10.已知(3x-5y-a)2+|x-1|=0中,y的值小于1,则a的取值范围是( )
| A. | a<-2 | B. | a>-2 | C. | a<8 | D. | 无法确定 |
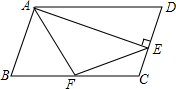 已知?ABCD中,AD=2AB,F是BC的中点,作AE⊥CD,垂足E在线段CD上,连结EF、AF,下列结论:①2∠BAF=∠BAD;②EF=AF;③S△ABF≤S△AEF;④∠BFE=3∠CEF.中一定成立的是( )
已知?ABCD中,AD=2AB,F是BC的中点,作AE⊥CD,垂足E在线段CD上,连结EF、AF,下列结论:①2∠BAF=∠BAD;②EF=AF;③S△ABF≤S△AEF;④∠BFE=3∠CEF.中一定成立的是( )