题目内容
14.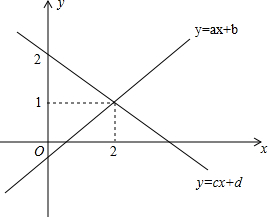 如图,直线y=ax+b与直线y=cx+d相交于点(2,1),则关于x的一元一次方程ax+b=cx+d的解为x=2.
如图,直线y=ax+b与直线y=cx+d相交于点(2,1),则关于x的一元一次方程ax+b=cx+d的解为x=2.
分析 由直线y=ax+b与直线y=cx+d相交于点(2,1),可知点(2,1)既在直线y=ax+b上,又在直线y=cx+d上,即x=2时,ax+b=cx+d,所以关于x的一元一次方程ax+b=cx+d的解为x=2.
解答 解:∵直线y=ax+b与直线y=cx+d相交于点(2,1),
∴x=2时,ax+b=1,cx+d=1,即ax+b=cx+d,
∴关于x的一元一次方程ax+b=cx+d的解为x=2.
故答案为x=2.
点评 本题考查了一次函数与一元一次方程,利用数形结合是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.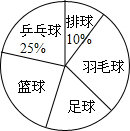 某中学为合理安排体育活动,在全校喜欢乒乓球、排球、羽毛球、足球、篮球五种球类运动的500名学生中,随机抽取了若干名学生进行调查,了解学生最喜爱的一种球类运动,每人只能在这五种球类运动中选择一种.调查结果统计如下:
某中学为合理安排体育活动,在全校喜欢乒乓球、排球、羽毛球、足球、篮球五种球类运动的500名学生中,随机抽取了若干名学生进行调查,了解学生最喜爱的一种球类运动,每人只能在这五种球类运动中选择一种.调查结果统计如下:
解答下列问题:
(1)a=30,b=24;
(2)试估计上述500名学生中最喜欢羽毛球运动的人数;
(3)该学校将组织趣味运动会,九(1)班决定从3名喜欢乒乓球、1名喜欢羽毛球,1名喜欢篮球的5名学生中随机抽取2人作为班级代表参加活动,那么被抽到的2名同学都是喜欢乒乓球的概率是多少?请用树状图或列表法说明理由.
 某中学为合理安排体育活动,在全校喜欢乒乓球、排球、羽毛球、足球、篮球五种球类运动的500名学生中,随机抽取了若干名学生进行调查,了解学生最喜爱的一种球类运动,每人只能在这五种球类运动中选择一种.调查结果统计如下:
某中学为合理安排体育活动,在全校喜欢乒乓球、排球、羽毛球、足球、篮球五种球类运动的500名学生中,随机抽取了若干名学生进行调查,了解学生最喜爱的一种球类运动,每人只能在这五种球类运动中选择一种.调查结果统计如下:| 球类名称 | 乒乓球 | 排球 | 羽毛球 | 足球 | 篮球 |
| 人数 | a | 12 | 36 | 18 | b |
(1)a=30,b=24;
(2)试估计上述500名学生中最喜欢羽毛球运动的人数;
(3)该学校将组织趣味运动会,九(1)班决定从3名喜欢乒乓球、1名喜欢羽毛球,1名喜欢篮球的5名学生中随机抽取2人作为班级代表参加活动,那么被抽到的2名同学都是喜欢乒乓球的概率是多少?请用树状图或列表法说明理由.
5.64的平方根是( )
| A. | ±8 | B. | ±4 | C. | 8 | D. | 32 |
2.下列各数中,属于无理数的是( )
| A. | 12 | B. | $\frac{1}{3}$ | C. | $\sqrt{4}$ | D. | $\sqrt{5}$ |
3.下列式子正确的是( )
| A. | x6÷x3=x2 | B. | (-1)-1=-1 | C. | 4m-2=$\frac{1}{{4{m^2}}}$ | D. | (a2)4=a6 |
4.已知圆的面积为7π,估计该圆的半径r所在范围正确的是( )
| A. | 1<r<2 | B. | 2<r<3 | C. | 3<r<4 | D. | 4<r<5 |
 已知射线OC是∠AOB的角平分线.
已知射线OC是∠AOB的角平分线.