题目内容
20.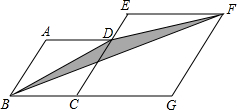 如图,菱形ABCD和菱形ECGF的边长分别为2和4,∠A=120°.则阴影部分面积是$\sqrt{3}$.(结果保留根号)
如图,菱形ABCD和菱形ECGF的边长分别为2和4,∠A=120°.则阴影部分面积是$\sqrt{3}$.(结果保留根号)
分析 设BF交CE于点H,根据菱形的对边平行,利用相似三角形对应边成比例列式求出CH,然后求出DH,根据菱形邻角互补求出∠ABC=60°,再求出点B到CD的距离以及点G到CE的距离;然后根据阴影部分的面积=S△BDH+S△FDH,根据三角形的面积公式列式进行计算即可得解.
解答 解:如图,设BF交CE于点H,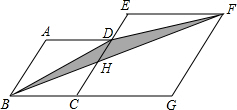
∵菱形ECGF的边CE∥GF,
∴△BCH∽△BGF,
∴$\frac{CH}{FG}=\frac{BC}{BG}$,
即$\frac{CH}{4}=\frac{2}{2+4}$,
解得CH=$\frac{4}{3}$,
所以,DH=CD-CH=2-$\frac{4}{3}=\frac{2}{3}$,
∵∠A=120°,
∴∠ECG=∠ABC=180°-120°=60°,
∴点B到CD的距离为2×$\frac{\sqrt{3}}{2}=\sqrt{3}$,
点G到CE的距离为4×$\frac{\sqrt{3}}{2}=2\sqrt{3}$,
∴阴影部分的面积=S△BDH+S△FDH,
=$\frac{1}{2}×\frac{2}{3}×\sqrt{3}+\frac{1}{2}×\frac{2}{3}×2\sqrt{3}$,
=$\sqrt{3}$.
故答案为:$\sqrt{3}$
点评 本题考查了菱形的对边平行,邻角互补的性质,相似三角形对应边成比例的性质,求出DH的长度,把阴影部分的面积分成两个三角形的面积进行求解是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.一元二次方程x2-3x-5=0的根的情况是( )
| A. | 有两个相等的实数根 | B. | 没有实数根 | ||
| C. | 无法确定是否有实数根 | D. | 有两个不相等的实数根 |
5.64的平方根是( )
| A. | ±8 | B. | ±4 | C. | 8 | D. | 32 |
10.已知(3x-5y-a)2+|x-1|=0中,y的值小于1,则a的取值范围是( )
| A. | a<-2 | B. | a>-2 | C. | a<8 | D. | 无法确定 |
