题目内容
11.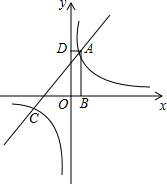 如图,矩形ABCD的顶点A是函数y=$\frac{k}{x}$的图象与函数y=x+(k-1)的图象在第一象限的交点,两函数图象另一交点为点C,AB垂直于x轴,垂足为点B,AD垂直于y轴,垂足为点D,且矩形ABOD的面积为5.
如图,矩形ABCD的顶点A是函数y=$\frac{k}{x}$的图象与函数y=x+(k-1)的图象在第一象限的交点,两函数图象另一交点为点C,AB垂直于x轴,垂足为点B,AD垂直于y轴,垂足为点D,且矩形ABOD的面积为5.(1)求两函数的解析;
(2)求交点A、C的坐标;
(3)连接OA、OC,求△AOC的面积S△AOC.
分析 (1)根据反比例函数的性质,可知矩形面积=|k|解决.
(2)列方程组求交点坐标.
(3)利用S△AOC=S△OMC+S△OMA求解.
解答 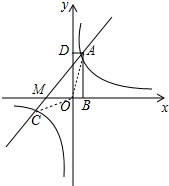 解:如图,
解:如图,
(1)∵矩形ABOD的面积为5,
∴k=5,
∴两函数的解析式分别为:y=$\frac{5}{x}$,y=x+4,.
(2)由$\left\{\begin{array}{l}{y=\frac{5}{x}}\\{y=x+4}\end{array}\right.$解得$\left\{\begin{array}{l}{x=1}\\{y=5}\end{array}\right.或\left\{\begin{array}{l}{x=-5}\\{y=-1}\end{array}\right.$
则点A(1,5),点C(-5,-1).
(3)∵直线AC与x轴交于点M(-4,0),
∴S△AOC=S△OMC+S△OMA=$\frac{1}{2}$×4×1+$\frac{1}{2}$×4×5=12.
点评 本题考查反比例函数性质、一次函数的性质,知道两个函数的交点用解方程组的思想解决,理解用分割法求三角形面积.

练习册系列答案
相关题目
3.分解因式2x2-4x的最终结果是( )
| A. | 2(x2-2x) | B. | x(2x2-4) | C. | 2x(x-2) | D. | 2x(x-4) |
20.一扇形的半径等于已知圆的半径的3倍,且它的面积等于该圆的面积,则这一扇形的圆心角为( )
| A. | 20° | B. | 120° | C. | 100° | D. | 40° |
1.已知直线y=3x-3与y=-$\frac{3}{2}$x+b的交点的坐标为($\frac{4}{3}$,a),则方程组$\left\{{\begin{array}{l}{-3x+y+3=0}\\{3x+2y-2b=0}\end{array}}$的解是( )
| A. | $\left\{{\begin{array}{l}{x=\frac{4}{3}}\\{y=-1}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{x=\frac{4}{3}}\\{y=1}\end{array}}\right.$ | C. | $\left\{{\begin{array}{l}{x=-\frac{4}{3}}\\{y=-1}\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}{x=1}\\{y=\frac{4}{3}}\end{array}}\right.$ |
 由四个相同的小正方形拼成如图,能否将连续的24个自然数分别放在图中所示的24个黑点处(每处放一个,每个数只使用一次)使得图中所有正方形边上所放的数之和都相等?若能,请给出一个例子;若不能,请说明理由.
由四个相同的小正方形拼成如图,能否将连续的24个自然数分别放在图中所示的24个黑点处(每处放一个,每个数只使用一次)使得图中所有正方形边上所放的数之和都相等?若能,请给出一个例子;若不能,请说明理由. 如图所示:所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长是13m,则正方形A、B、C、D的面积之和是169m2.
如图所示:所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长是13m,则正方形A、B、C、D的面积之和是169m2. 如图,在Rt△ABC中,∠ACB=90°.
如图,在Rt△ABC中,∠ACB=90°.