题目内容
1.已知直线y=3x-3与y=-$\frac{3}{2}$x+b的交点的坐标为($\frac{4}{3}$,a),则方程组$\left\{{\begin{array}{l}{-3x+y+3=0}\\{3x+2y-2b=0}\end{array}}$的解是( )| A. | $\left\{{\begin{array}{l}{x=\frac{4}{3}}\\{y=-1}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{x=\frac{4}{3}}\\{y=1}\end{array}}\right.$ | C. | $\left\{{\begin{array}{l}{x=-\frac{4}{3}}\\{y=-1}\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}{x=1}\\{y=\frac{4}{3}}\end{array}}\right.$ |
分析 把交点坐标代入y=3x-3求解得到a的值,再根据方程组的解即为交点坐标解答.
解答 解:∵把($\frac{4}{3}$,a)代入y=3x-3,
∴得a=3×$\frac{4}{3}$-3=1,
∴直线y=3x-3与y=-$\frac{3}{2}$x+b的交点的坐标为($\frac{4}{3}$,1),
∴方程组$\left\{\begin{array}{l}{y=3x-3}\\{y=-\frac{3}{2}x+b}\end{array}\right.$即$\left\{{\begin{array}{l}{-3x+y+3=0}\\{3x+2y-2b=0}\end{array}}$的解为$\left\{\begin{array}{l}{x=\frac{4}{3}}\\{y=1}\end{array}\right.$.
故选B.
点评 本题主要考查了一次函数和二元一次方程组的关系,满足解析式的点就在函数的图象上,在函数的图象上的点,就一定满足函数解析式.函数图象交点坐标为两函数解析式组成的方程组的解.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
12.一学员在广场上练习驾驶汽车,两次拐弯后,行驶方向与原来的方向相同,这两次拐弯的角度可能是( )
| A. | 第一次向右拐50°第二次向左拐130° | |
| B. | 第一次向左拐30°第二次向右拐30° | |
| C. | 第一次向右拐50°第二次向右拐130° | |
| D. | 第一次向左拐50°第二次向左拐130° |
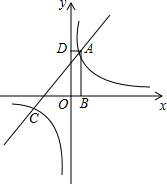 如图,矩形ABCD的顶点A是函数y=$\frac{k}{x}$的图象与函数y=x+(k-1)的图象在第一象限的交点,两函数图象另一交点为点C,AB垂直于x轴,垂足为点B,AD垂直于y轴,垂足为点D,且矩形ABOD的面积为5.
如图,矩形ABCD的顶点A是函数y=$\frac{k}{x}$的图象与函数y=x+(k-1)的图象在第一象限的交点,两函数图象另一交点为点C,AB垂直于x轴,垂足为点B,AD垂直于y轴,垂足为点D,且矩形ABOD的面积为5.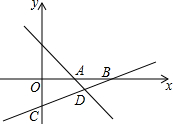 如图,直线l1:y=-x+3与x轴相交于点A,直线l2:y=kx+b经过点(3,-1),与x轴交于点B(6,0),与y轴交于点C,与直线l1相交于点D.
如图,直线l1:y=-x+3与x轴相交于点A,直线l2:y=kx+b经过点(3,-1),与x轴交于点B(6,0),与y轴交于点C,与直线l1相交于点D. 如图,请按照要求回答问题.
如图,请按照要求回答问题. 如图,在△ABC中,AB=AC,D,E分别是AB,AC的中点,且CD,BE交于O点.求证:BO=CO.
如图,在△ABC中,AB=AC,D,E分别是AB,AC的中点,且CD,BE交于O点.求证:BO=CO.