题目内容
6. 如图,在Rt△ABC中,∠ACB=90°.
如图,在Rt△ABC中,∠ACB=90°.(1)用尺规在边BC上求作一点P,使PA=PB(不写作法,保留作图痕迹);
(2)连结AP,若AC=4,BC=8时,试求BP的长.
分析 (1)作AB的垂直平分线交BC于P点,则PA=PB;
(2)设BP=x,则AP=x,CP=BC-PB=8-x,然后在Rt△ACP中根据勾股定理得到(8-x)2+42=x2,再解方程即可.
解答 解:(1)如图,点P为所作;
(2)设BP=x,则AP=x,CP=BC-PB=8-x,
在Rt△ACP中,∵PC2+AC2=AP2,
∴(8-x)2+42=x2,解得x=5,
即BP的长为5.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
16.点(3,y1)、(5,y2)在二次函数y=$\frac{1}{2}$x2-x-$\frac{3}{8}$的图象上,判断y1、y2的大小关系正确的是( )
| A. | y1<y2 | B. | y1>y2 | C. | y1=y2 | D. | 不能判定 |
15.下列事件中,必然事件是( )
| A. | 抛出一枚硬币,落地后正面向上 | |
| B. | 打开电视,正在播放广告 | |
| C. | 篮球队员在罚球线投篮一次,未投中 | |
| D. | 实心铁球投入水中会沉入水底 |

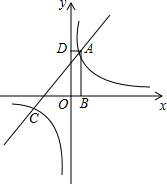 如图,矩形ABCD的顶点A是函数y=$\frac{k}{x}$的图象与函数y=x+(k-1)的图象在第一象限的交点,两函数图象另一交点为点C,AB垂直于x轴,垂足为点B,AD垂直于y轴,垂足为点D,且矩形ABOD的面积为5.
如图,矩形ABCD的顶点A是函数y=$\frac{k}{x}$的图象与函数y=x+(k-1)的图象在第一象限的交点,两函数图象另一交点为点C,AB垂直于x轴,垂足为点B,AD垂直于y轴,垂足为点D,且矩形ABOD的面积为5.