题目内容
19．
如图所示：所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长是13m，则正方形A、B、C、D的面积之和是169m2．
分析 根据正方形的面积公式，运用勾股定理可以证明：四个小正方形的面积和等于最大正方形的面积即169．
解答 
解：根据勾股定理得到：C与D的面积的和是P的面积；A与B的面积的和是Q的面积；而P，Q的面积的和是M的面积．
即A、B、C、D的面积之和为M的面积．
∵M的面积是132=169，
∴A、B、C、D的面积之和为169m2．
故答案为：169m2．
点评 本题考查了勾股定理的应用．能够发现正方形A，B，C，D的边长正好是两个直角三角形的四条直角边，根据勾股定理最终能够证明正方形A，B，C，D的面积和即是最大正方形的面积．
练习册系列答案
阳光课堂课时作业系列答案
相关题目
9．下列运算正确的是（ ）
| A． | -40=1 | B． | （-3）-1=$\frac{1}{3}$ | C． | （-2m-n）2=4m-n | D． | （a+b）-1=a-1+b-1 |
10．公司9月份利润为100万元，要使11月份的利润达到144万元，则平均每月增长的百分率为（ ）
| A． | 10% | B． | 20% | C． | 22% | D． | 25% |
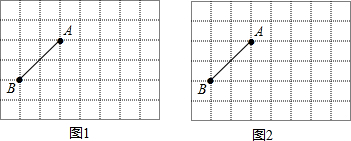
等腰△ABC的底边上高AD与底角平分线CE交于点P，EF⊥AD，F为垂足，若线段EB=4，则线段EF=2．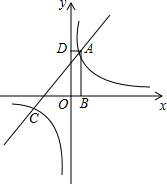
如图，矩形ABCD的顶点A是函数y=$\frac{k}{x}$的图象与函数y=x+（k-1）的图象在第一象限的交点，两函数图象另一交点为点C，AB垂直于x轴，垂足为点B，AD垂直于y轴，垂足为点D，且矩形ABOD的面积为5．