题目内容
17.(1)分解因式:3x3-12x2y+12xy2.(2)先化简,再求值:$\frac{2x-6}{x-2}$÷($\frac{5}{x-2}$-x-2),其中x=-2.
分析 (1)先提取公因式,再利用完全平方公式把原式进行因式分解即可;
(2)先根据分式混合运算的法则把原式进行化简,再把x的值代入进行计算即可.
解答 解:(1)原式=3x(x2-4xy+4y2 )
=3x(x-2y)2;
(2)原式=$\frac{2(x-3)}{x-2}$÷$\frac{9-{x}^{2}}{x-2}$
=$\frac{2(x-3)}{x-2}$×$\frac{x-2}{-(x-3)(x+3)}$
=-$\frac{2}{x+3}$,
当x=-2时,原式=-2.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
8.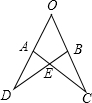 如图,OA=OB,OC=OD,∠O=50°,∠D=35°,则∠OAC等于( )
如图,OA=OB,OC=OD,∠O=50°,∠D=35°,则∠OAC等于( )
 如图,OA=OB,OC=OD,∠O=50°,∠D=35°,则∠OAC等于( )
如图,OA=OB,OC=OD,∠O=50°,∠D=35°,则∠OAC等于( )| A. | 65° | B. | 95° | C. | 45° | D. | 100° |
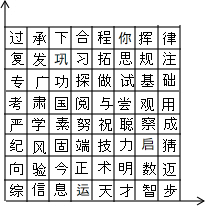 如图是一组密码的一部分,为了保密,许多情况下课采用不同的密码,请你运用所学知识找到破译的“钥匙”.目前,已破译出“正做数学”的真实意思是“祝你成功”.若“正”所处的位置为(x,y),你找到的密码钥匙是对应文字横坐标加1,纵坐标加2,破译的“今天考试”真实意思是“努力发挥”.
如图是一组密码的一部分,为了保密,许多情况下课采用不同的密码,请你运用所学知识找到破译的“钥匙”.目前,已破译出“正做数学”的真实意思是“祝你成功”.若“正”所处的位置为(x,y),你找到的密码钥匙是对应文字横坐标加1,纵坐标加2,破译的“今天考试”真实意思是“努力发挥”. 如图,已知CD⊥AB于点D,FE⊥AB于点E,且∠1=∠2,∠DGC=96°,求∠ACB的度数.
如图,已知CD⊥AB于点D,FE⊥AB于点E,且∠1=∠2,∠DGC=96°,求∠ACB的度数. 如图所示,△A′B′C′是△ABC经过平移得到的,A(-4,-1),B(-5,-4),C(-1,-3),△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4).
如图所示,△A′B′C′是△ABC经过平移得到的,A(-4,-1),B(-5,-4),C(-1,-3),△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4). 如图,A、C在?BFDE的对角线EF所在的直线上,且AE=CF,求证:BC∥AD.
如图,A、C在?BFDE的对角线EF所在的直线上,且AE=CF,求证:BC∥AD.