题目内容
 如图,菱形ABCD的周长40cm,它的一条对角线BD长10cm.
如图,菱形ABCD的周长40cm,它的一条对角线BD长10cm.(1)求∠DAB的度数;
(2)求菱形另一条对角线AC的长.
考点:菱形的性质
专题:
分析:(1)分别求出菱形的边长AD和OD的长度,然后利用三角函数求解∠DAO的度数,继而可得解;
(2)直接根据勾股定理求出AO的长度,继而可求得AC的长度.
(2)直接根据勾股定理求出AO的长度,继而可求得AC的长度.
解答:解:(1)∵菱形的周长为40cm,BD=10cm,
∴AD=10cm,OD=5cm,
则sin∠DAO=
=
,
∴∠DAO=30°,
∴∠DAB=2×30°=60°;
(2)AO=
=5
,
则AC=2×5
=10
(cm).
即菱形另一条对角线AC的长为10
cm.
∴AD=10cm,OD=5cm,
则sin∠DAO=
| OD |
| AD |
| 1 |
| 2 |
∴∠DAO=30°,
∴∠DAB=2×30°=60°;
(2)AO=
| AD2-DO2 |
| 3 |
则AC=2×5
| 3 |
| 3 |
即菱形另一条对角线AC的长为10
| 3 |
点评:本题考查了菱形的性质,解答本题的关键掌握菱形四条边都相等和两条对角线互相垂直,并且每一条对角线平分一组对角.

练习册系列答案
相关题目
如图所示,阴影部分面积最大的是( )
A、 |
B、 |
C、 |
D、 |
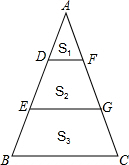 如图,D、E是AB的三等分点,且DF∥EG∥BC,则图中三部分图形的面积比S1:S2:S3=( )
如图,D、E是AB的三等分点,且DF∥EG∥BC,则图中三部分图形的面积比S1:S2:S3=( )| A、1:2:3 |
| B、1:4:9 |
| C、1:3:5 |
| D、1:3:6 |
 如图,在△ABC中,AB=AC=5,AB的重直平分线DE交AB、AC于E、D,△BCD的周长为8,求△ABC的周长.
如图,在△ABC中,AB=AC=5,AB的重直平分线DE交AB、AC于E、D,△BCD的周长为8,求△ABC的周长. 如图,B,C,D是线段AE上的三个点,已知AE=9,BD=4,求图中以A、B、C、D、E这5个点为端点的所有线段的和为
如图,B,C,D是线段AE上的三个点,已知AE=9,BD=4,求图中以A、B、C、D、E这5个点为端点的所有线段的和为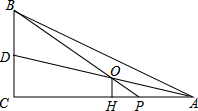 如图,在△ABC中,∠C=90°,AC=8,AB=10,点P在AC上,AP=2,若AD平分∠BAC,且AD与BP相交于点O,OH⊥AC,计算线段OH的长度?
如图,在△ABC中,∠C=90°,AC=8,AB=10,点P在AC上,AP=2,若AD平分∠BAC,且AD与BP相交于点O,OH⊥AC,计算线段OH的长度?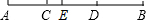 如图,点C为线段AB上的一点,AC=
如图,点C为线段AB上的一点,AC=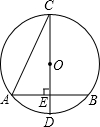 如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,连接BC,若AB=2
如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,连接BC,若AB=2