题目内容
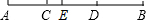 如图,点C为线段AB上的一点,AC=
如图,点C为线段AB上的一点,AC=| 1 |
| 3 |
(1)若AB=16,求DC的长;
(2)若E为AD的中点,且CE=1.5,求AB的长.
考点:两点间的距离
专题:
分析:(1)设AC=x,则BC=3x,再根据D为BC的中点可用x表示出DC的长,再根据AB=16求出x的值,进而可得出结论;
(2)根据CE=AE-AC用x表示出CE的长,根据CE=1.5求出x的值,进而可得出AB的长.
(2)根据CE=AE-AC用x表示出CE的长,根据CE=1.5求出x的值,进而可得出AB的长.
解答:解:(1)∵点C为线段AB上的一点,AC=
BC,
∴设AC=x,则BC=3x.
∵D为BC的中点,
∴CD=
BC=
x.
∵AB=AC+BC=x+3x=16,
∴x=4,
∴CD=
BC=
×4=6;
(2)∵由(1)知,CD=
x,AB=AC+BC=x+3x=4x,
∴AD=AC+CD=x+
x=
x.
∵E为AD的中点,
∴AE=
AD=
×
x=
x.
∵CE=1.5,
∴CE=AE-AC=
x-x=1.5,解得x=6,
∴AB=4x=4×6=24.
| 1 |
| 3 |
∴设AC=x,则BC=3x.
∵D为BC的中点,
∴CD=
| 1 |
| 2 |
| 3 |
| 2 |
∵AB=AC+BC=x+3x=16,
∴x=4,
∴CD=
| 1 |
| 2 |
| 3 |
| 2 |
(2)∵由(1)知,CD=
| 3 |
| 2 |
∴AD=AC+CD=x+
| 3 |
| 2 |
| 5 |
| 2 |
∵E为AD的中点,
∴AE=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 5 |
| 4 |
∵CE=1.5,
∴CE=AE-AC=
| 5 |
| 4 |
∴AB=4x=4×6=24.
点评:本题考查的是两点间的距离,熟知各线段之间的和、差及倍数关系是解答此题的关键.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
 如图,菱形ABCD的周长40cm,它的一条对角线BD长10cm.
如图,菱形ABCD的周长40cm,它的一条对角线BD长10cm. 利用圆规和直尺分别作圆内接正三角形和圆内接正四边形.
利用圆规和直尺分别作圆内接正三角形和圆内接正四边形. 如图,四边形ABCD是长方形(长方形对边相等且平行,四个角为直角),
如图,四边形ABCD是长方形(长方形对边相等且平行,四个角为直角),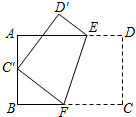 如图,将矩形ABCD沿EF折叠,使顶点C落在AB边的中点c,上.若AB=6,BC=9,则BF的长为
如图,将矩形ABCD沿EF折叠,使顶点C落在AB边的中点c,上.若AB=6,BC=9,则BF的长为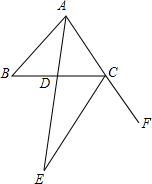 如图,已知∠ABC=31°,又△BAC的角平分线AE与∠BCA的外角平分线CE相交于E点,则∠AEC为
如图,已知∠ABC=31°,又△BAC的角平分线AE与∠BCA的外角平分线CE相交于E点,则∠AEC为