题目内容
3.如图,将?ABCD的边DC延长到点E,使CE=DC,连接AC、BE.(1)如图1,求证:四边形ABEC为平行四边形;
(2)如图2,连接AE,若AE⊥BC,请直接写出图2中的所有等腰三角形.
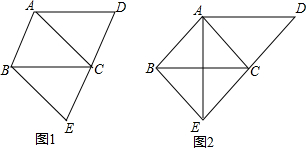
分析 (1)由平行四边形的性质得出AB∥CD,AB=CD,再由已知条件得出AB=CE,即可得出结论;
(2)证明四边形ABEC是菱形,得出AB=BE=EC=AC,得出△ABC、△BCE、△ABE、△ACE是等腰三角形,再证出AC=CD,得出△ACD是等腰三角形.
解答 (1)证明:∵四边形ABCD为平行四边形,
∴AB∥CD,AB=CD,
∵CE=CD,
∴AB=CE,
∴四边形ABEC是平行四边形;
(2)解:等腰三角形有:△ABC、△BCE、△ABE、△ACE、△ACD;理由如下:
∵四边形ABEC是平行四边形,
∵AE⊥BC,
∴四边形ABEC是菱形,
∴AB=BE=EC=AC,
∴△ABC、△BCE、△ABE、△ACE是等腰三角形,
又∵四边形ABCD为平行四边形,
∴AB=CD,
∴AC=CD,
∴△ACD是等腰三角形.
点评 本题考查了平行四边形的性质与判定、菱形的判定与性质、等腰三角形的判定;熟练掌握平行四边形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
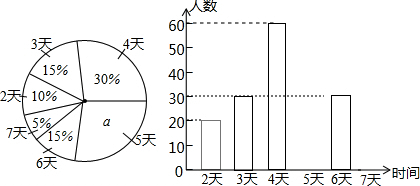
14. 某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分,80分,90分,100分,并根据统计数据绘制了如下不完整的统计图表:
某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分,80分,90分,100分,并根据统计数据绘制了如下不完整的统计图表:
乙校成绩统计表
(1)在图①中,“80分”所在扇形的圆心角度数为54°;
(2)请你将图②补充完整;
(3)求乙校成绩的平均分;
(4)经计算知S甲2=135,S乙2=175,请你根据这两个数据,对甲、乙两校成绩作出合理评价.
 某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分,80分,90分,100分,并根据统计数据绘制了如下不完整的统计图表:
某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分,80分,90分,100分,并根据统计数据绘制了如下不完整的统计图表:乙校成绩统计表
| 分数(分) | 人数(人) |
| 70 | 7 |
| 80 | |
| 90 | 1 |
| 100 | 8 |
(2)请你将图②补充完整;
(3)求乙校成绩的平均分;
(4)经计算知S甲2=135,S乙2=175,请你根据这两个数据,对甲、乙两校成绩作出合理评价.
18.已知x1,x2是一元二次方程x2-4x+1=0的两个实数根,则x1x2-x1-x2的值等于( )
| A. | -3 | B. | 0 | C. | 3 | D. | 5 |
12.洛阳市某家电商场要购进一批电视机和洗衣机,根据市场调查,决定电视机进货量不少于洗衣机进货量的一半,电视机与洗衣机的进价和售价如表:
计划购进电视机和洗衣机共100台,商店最多可筹资金141000元.
(1)请你帮助商场算一算有多少进货方案?(不考虑除进价之外的其它费用)
(2)哪种进货方案待商店销售完购进的电视机与洗衣机后获得利润最多?并求出最多利润.(利润=售价-进价)
| 类别 | 电视机 | 洗衣机 |
| 进价(元/台) | 1600 | 1300 |
| 售价(元/台) | 1800 | 1400 |
(1)请你帮助商场算一算有多少进货方案?(不考虑除进价之外的其它费用)
(2)哪种进货方案待商店销售完购进的电视机与洗衣机后获得利润最多?并求出最多利润.(利润=售价-进价)
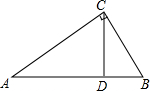 如图,在直角三角形ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B.
如图,在直角三角形ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B.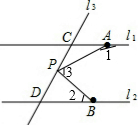 如图,已知直线l1∥l2,A、B分别是l1、l2上的点,l3和l1、l2分别交于点C、D,点P是线段CD上的动点(点P不与C、D重合).
如图,已知直线l1∥l2,A、B分别是l1、l2上的点,l3和l1、l2分别交于点C、D,点P是线段CD上的动点(点P不与C、D重合). 已知,如图,CE是△ABC的角平分线,点D、F分别在AC、BC上,且DE∥BC,DF∥AB.
已知,如图,CE是△ABC的角平分线,点D、F分别在AC、BC上,且DE∥BC,DF∥AB.