题目内容
19.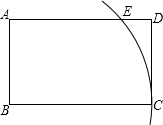 如图,在矩形ABCD中,$\frac{AB}{BC}=\frac{3}{5}$,以点B为圆心,BC长为半径画弧,交边AD于点E.若AE•ED=8,则矩形ABCD的面积为30.
如图,在矩形ABCD中,$\frac{AB}{BC}=\frac{3}{5}$,以点B为圆心,BC长为半径画弧,交边AD于点E.若AE•ED=8,则矩形ABCD的面积为30.
分析 连接BE,设AB=3x,BC=5x,根据勾股定理求出AE=4x,DE=x,求出x的值,求出AB、BC,即可求出答案.
解答 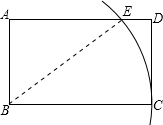 解:如图,连接BE,则BE=BC.
解:如图,连接BE,则BE=BC.
设AB=3x,BC=5x,
∵四边形ABCD是矩形,
∴AB=CD=3x,AD=BC=5x,∠A=90°,
由勾股定理得:AE=4x,
则DE=5x-4x=x,
∵AE•ED=8,
∴4x•x=8,
解得:x=$\sqrt{2}$,
则AB=3x=3$\sqrt{2}$,BC=5x=5$\sqrt{2}$,
∴矩形ABCD的面积是AB×BC=3$\sqrt{2}$×5$\sqrt{2}$=30,
故答案为:30.
点评 本题考查了矩形的性质,勾股定理的应用,解此题的关键是表示出AE、ED,利用方程思想求出x的值.

练习册系列答案
相关题目
7. 如图,直线a∥b,则∠ABD的度数是( )
如图,直线a∥b,则∠ABD的度数是( )
 如图,直线a∥b,则∠ABD的度数是( )
如图,直线a∥b,则∠ABD的度数是( )| A. | 80° | B. | 100° | C. | 112° | D. | 132° |
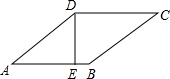 如图,菱形ABCD的周长为20cm,DE⊥AB,垂足为E,$\frac{AE}{AD}=\frac{4}{5}$,下列结论:
如图,菱形ABCD的周长为20cm,DE⊥AB,垂足为E,$\frac{AE}{AD}=\frac{4}{5}$,下列结论: 阅读下列材料:
阅读下列材料: 如图是我国古代数学家杨辉最早发现的,称为“杨辉三角”.“杨辉三角”中有许多规律,如它的每一行的数字正好对应了(a+b)n(n为非负整数)的展开式中a按次数从大到小排列的项的系数.例如,(a+b)2=a2+2ab+b2展开式中的系数1、2、1恰好对应图中第三行的数字.请认真观察此图,写出(a+b)3的展开式(a+b)3=a3+3a2b+3ab2+b3.
如图是我国古代数学家杨辉最早发现的,称为“杨辉三角”.“杨辉三角”中有许多规律,如它的每一行的数字正好对应了(a+b)n(n为非负整数)的展开式中a按次数从大到小排列的项的系数.例如,(a+b)2=a2+2ab+b2展开式中的系数1、2、1恰好对应图中第三行的数字.请认真观察此图,写出(a+b)3的展开式(a+b)3=a3+3a2b+3ab2+b3.
 如图,在菱形ABCD中,AB=2,∠ABC=60°,对角线AC、BD相交于点O,将对角线AC所在的直线绕点O顺时针旋转角α(0°<α<90°)后得直线l,直线l与AD、BC两边分别相交于点E和点F.
如图,在菱形ABCD中,AB=2,∠ABC=60°,对角线AC、BD相交于点O,将对角线AC所在的直线绕点O顺时针旋转角α(0°<α<90°)后得直线l,直线l与AD、BC两边分别相交于点E和点F.