题目内容
9. 如图,在菱形ABCD中,AB=2,∠ABC=60°,对角线AC、BD相交于点O,将对角线AC所在的直线绕点O顺时针旋转角α(0°<α<90°)后得直线l,直线l与AD、BC两边分别相交于点E和点F.
如图,在菱形ABCD中,AB=2,∠ABC=60°,对角线AC、BD相交于点O,将对角线AC所在的直线绕点O顺时针旋转角α(0°<α<90°)后得直线l,直线l与AD、BC两边分别相交于点E和点F.(1)求证:△AOE≌△COF;
(2)当α=30°时,求线段EF的长度.
分析 (1)首先证明AE=CF,OE=OF,结合AO=CO,利用SSS证明△AOE≌△COF;
(2)首先画出α=30°时的图形,根据菱形的性质得到EF⊥AD,解三角形即可求出OE的长,进而得到EF的长.
解答  解:(1)∵四边形ABCD是菱形,
解:(1)∵四边形ABCD是菱形,
∴AD∥BC,AO=OC,
∴$\frac{AE}{CF}=\frac{OE}{OF}=\frac{AO}{OC}=1$,
∴AE=CF,OE=OF,
在△AOE和△COF中,
$\left\{\begin{array}{l}{AO=CO}\\{OE=OF}\\{AE=CF}\end{array}\right.$
∴△AOE≌△COF.
(2)当α=30°时,即∠AOE=30°,
∵四边形ABCD是菱形,∠ABC=60°,
∴∠OAD=60°,
∴∠AEO=90°,
在Rt△AOB中,
sin∠ABO=$\frac{AO}{AB}$=$\frac{AO}{2}$=$\frac{1}{2}$,
∴AO=1,
在Rt△AEO中,
cos∠AOE=cos30°=$\frac{OE}{AO}$=$\frac{\sqrt{3}}{2}$,
∴OE=$\frac{\sqrt{3}}{2}$,
∴EF=2OE=$\sqrt{3}$.
点评 本题主要考查了菱形的性质以及解三角形的知识,解答本题的关键是熟练掌握菱形的性质,解答(2)问时需要正确作出图形,此题难度不大.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案
相关题目
4.为了改善住房条件,小亮的父母考察了某小区的A、B两套房.B房的面积比A房的面积大24平方米,两套楼房的总房价,A房和B房每平米的价格分别是平均价格的1.1倍和0.9倍.为了计算两套楼房的面积,小亮设A房的面积为x平方米,B房的面积为y平方米,根据以上信息得出了下列方程组,其中正确的是( )
| A. | $\left\{\begin{array}{l}{0.9x=1.1y}\\{y-x=24}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{1.1x=0.9y}\\{x-y=24}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{0.9x=1.1y}\\{x-y=24}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{1.1x=0.9y}\\{y-x=24}\end{array}\right.$ |
14. 如图,在坡角为30°的斜坡上要栽两棵树,要求它们之间的水平距离AC为6m,则这两棵树之间的坡面AB的长为( )
如图,在坡角为30°的斜坡上要栽两棵树,要求它们之间的水平距离AC为6m,则这两棵树之间的坡面AB的长为( )
 如图,在坡角为30°的斜坡上要栽两棵树,要求它们之间的水平距离AC为6m,则这两棵树之间的坡面AB的长为( )
如图,在坡角为30°的斜坡上要栽两棵树,要求它们之间的水平距离AC为6m,则这两棵树之间的坡面AB的长为( )| A. | 12m | B. | 3$\sqrt{3}$m | C. | 4$\sqrt{3}$m | D. | 12$\sqrt{3}$m |
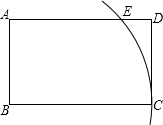 如图,在矩形ABCD中,$\frac{AB}{BC}=\frac{3}{5}$,以点B为圆心,BC长为半径画弧,交边AD于点E.若AE•ED=8,则矩形ABCD的面积为30.
如图,在矩形ABCD中,$\frac{AB}{BC}=\frac{3}{5}$,以点B为圆心,BC长为半径画弧,交边AD于点E.若AE•ED=8,则矩形ABCD的面积为30. 如图,已知二次函数L1:y=ax2-2ax+a+3(a>0)和二次函数L2:y=-a(x+1)2+1(a>0)图象的顶点分别为M,N,与y轴分别交于点E,F.
如图,已知二次函数L1:y=ax2-2ax+a+3(a>0)和二次函数L2:y=-a(x+1)2+1(a>0)图象的顶点分别为M,N,与y轴分别交于点E,F.