题目内容
14. 阅读下列材料:
阅读下列材料:我们定义:若一个四边形的一条对角线把四边形分成两个等腰三角形,则称这条对角线叫这个四边形的和谐线,这个四边形叫做和谐四边形.如正方形就是和谐四边形.
结合阅读材料,完成下列问题:
(1)下列哪个四边形一定是和谐四边形C
A.平行四边形 B.矩形 C.菱形 D.等腰梯形
(2)如图,等腰Rt△ABD中,∠BAD=90°.若点C为平面上一点,AC为凸四边形ABCD的和谐线,且AB=BC,请直接写出∠ABC的度数.
分析 (1)有和谐四边形的定义即可得到菱形是和谐四边形;
(2)首先根据题意画出图形,然后由AC是四边形ABCD的和谐线,可以得出△ACD是等腰三角形,从图1,图2,图3三种情况运用等边三角形的性质,正方形的性质和30°的直角三角形性质就可以求出∠ABC的度数.
解答  解:(1)∵菱形的四条边相等,
解:(1)∵菱形的四条边相等,
∴连接对角线能得到两个等腰三角形,
∴菱形是和谐四边形;
(2)解:∵AC是四边形ABCD的和谐线,
∴△ACD是等腰三角形,
在等腰Rt△ABD中,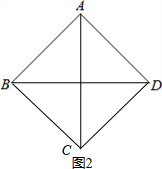
∵AB=AD,
∴AB=AD=BC,
如图1,当AD=AC时,
∴AB=AC=BC,∠ACD=∠ADC
∴△ABC是正三角形,
∴∠ABC=60°.
如图2,当AD=CD时,
∴AB=AD=BC=CD.
∵∠BAD=90°,
∴四边形ABCD是正方形,
∴∠ABC=90°;
如图3,当AC=CD时,过点C作CE⊥AD于E,过点B作BF⊥CE于F,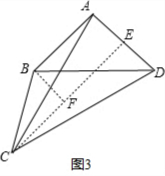
∵AC=CD.CE⊥AD,
∴AE=$\frac{1}{2}$AD,∠ACE=∠DCE.
∵∠BAD=∠AEF=∠BFE=90°,
∴四边形ABFE是矩形.
∴BF=AE.
∵AB=AD=BC,
∴BF=$\frac{1}{2}$BC,
∴∠BCF=30°.
∵AB=BC,
∴∠ACB=∠BAC.
∵AB∥CE,
∴∠BAC=∠ACE,
∴∠ACB=∠BAC=$\frac{1}{2}$∠BCF=15°,
∴∠ABC=150°,
综上:∠ABC的度数可能是:60°90°150°.
点评 此题考查了等腰直角三角形的性质,等腰三角形的性质、矩形的性质、正方形的性质,菱形的性质,此题难度较大,注意掌握数形结合思想与分类讨论思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4. 如图,将一张长方形纸条折叠,如果∠1=130°,则∠2=( )
如图,将一张长方形纸条折叠,如果∠1=130°,则∠2=( )
 如图,将一张长方形纸条折叠,如果∠1=130°,则∠2=( )
如图,将一张长方形纸条折叠,如果∠1=130°,则∠2=( )| A. | 100° | B. | 130° | C. | 150° | D. | 80° |
5. 七巧板被西方人称为“东方魔板”.如图的两幅图是由同一副七巧板拼成的.已知七巧板拼成的正方形的边长为8cm,则“一帆风顺”图中阴影部分的面积为( )
七巧板被西方人称为“东方魔板”.如图的两幅图是由同一副七巧板拼成的.已知七巧板拼成的正方形的边长为8cm,则“一帆风顺”图中阴影部分的面积为( )
 七巧板被西方人称为“东方魔板”.如图的两幅图是由同一副七巧板拼成的.已知七巧板拼成的正方形的边长为8cm,则“一帆风顺”图中阴影部分的面积为( )
七巧板被西方人称为“东方魔板”.如图的两幅图是由同一副七巧板拼成的.已知七巧板拼成的正方形的边长为8cm,则“一帆风顺”图中阴影部分的面积为( )| A. | 16cm2 | B. | 8cm2 | C. | 4cm2 | D. | 2cm2 |
6.舌尖上的浪费让人触目惊心!据统计,中国每年浪费的食物总量折合成粮食约为50000000000千克,把50000000000用科学记数法表示为( )
| A. | 5×1010 | B. | 50×109 | C. | 5×109 | D. | 0.5×1011 |
4.为了改善住房条件,小亮的父母考察了某小区的A、B两套房.B房的面积比A房的面积大24平方米,两套楼房的总房价,A房和B房每平米的价格分别是平均价格的1.1倍和0.9倍.为了计算两套楼房的面积,小亮设A房的面积为x平方米,B房的面积为y平方米,根据以上信息得出了下列方程组,其中正确的是( )
| A. | $\left\{\begin{array}{l}{0.9x=1.1y}\\{y-x=24}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{1.1x=0.9y}\\{x-y=24}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{0.9x=1.1y}\\{x-y=24}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{1.1x=0.9y}\\{y-x=24}\end{array}\right.$ |
 如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2),
如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2),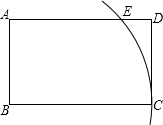 如图,在矩形ABCD中,$\frac{AB}{BC}=\frac{3}{5}$,以点B为圆心,BC长为半径画弧,交边AD于点E.若AE•ED=8,则矩形ABCD的面积为30.
如图,在矩形ABCD中,$\frac{AB}{BC}=\frac{3}{5}$,以点B为圆心,BC长为半径画弧,交边AD于点E.若AE•ED=8,则矩形ABCD的面积为30. 如图,在?ABCD中,对角线AC、BD相交成的锐角α为60°,若AC=10,BD=8,则?ABCD的面积是20$\sqrt{3}$.
如图,在?ABCD中,对角线AC、BD相交成的锐角α为60°,若AC=10,BD=8,则?ABCD的面积是20$\sqrt{3}$.