Question

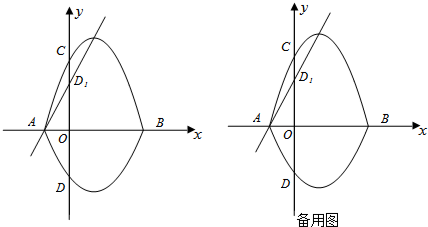
10．如图，在平面直角坐标系中，A、B为x轴上两点（点A在点B的左边），C、D为y轴上两点，经过A、C、B的抛物线的一部分C₁与经过A、D、B的抛物线的一部分C₂组合成一条封闭曲线，我们把这条封闭曲线称为“蛋线”．已知点D的坐标为（0，-2），抛物线C₁的解析式为y=mx²-2mx-3m（m＜0）．
（1）求A、B两点的坐标；
（2）若四边形ACBD是梯形，求m的值；
（3）若点D关于x轴的对称点为D₁，试判断直线AD₁与该蛋线的公共点的个数，并证明你的结论．

Answer 1

分析 （1）在函数y=mx²-2mx-3m中，令y=0，则mx²-2mx-3m=0，根据m＜0可知x²-2x-3=0，由此可得出AB两点的坐标；
（2）先根据A，B，D三点的坐标得出AO，BO，DO的长，在函数y=mx²-2mx-3m（m＜0）中，令x=0，则y=-3m，故可得出C点坐标，再分AC∥BD，BC∥AD两种情况进行分类讨论；
（3）根据点D₁与点D关于x轴对称可得出D₁的坐标，故可得出直线AD₁的方程，易知直线AD₁与抛物线C₂只有一个公共点A，联立直线AD₁和抛物线C₁的方程可得出x₁，x₂=-1的值，由m＜0，可知3+$\frac{2}{m}$＜3，再分当3+$\frac{2}{m}$＞-1与3+$\frac{2}{m}$≤-1两种情况进行讨论即可．

解答 解：（1）在函数y=mx²-2mx-3m中，令y=0，则mx²-2mx-3m=0，
∵m＜0，
∴x²-2x-3=0，
解得 x₁=3，x₂=-1．
∴A（-1，0），B（3，0）；

（2）∵A（-1，0），B（3，0），D（0，-2），
∴AO=1，BO=3，DO=2．
在函数y=mx²-2mx-3m（m＜0）中，令x=0，则y=-3m，
∴C（0，-3m），
则OC=-3m．
①若AC∥BD，则△AOC∽△BOD，
∴$\frac{AO}{CO}$=$\frac{BO}{DO}$，
∴$\frac{1}{-3m}$=$\frac{3}{2}$，
解得m=-$\frac{2}{9}$，
此时AC≠BD，四边形ACBD是梯形．
②若BC∥AD，
则△AOD∽△BOC，
∴$\frac{AO}{DO}$=$\frac{BO}{CO}$，
∴$\frac{1}{2}$=$\frac{3}{-3m}$，
解得m-2，
此时AD≠BC，四边形ACBD是梯形．
综上所述，m=-$\frac{2}{9}$或-2．

（3）∵点D₁与点D关于x轴对称，
∴D₁（0，2）．
则直线AD₁的方程为：y=2x+2，
易知直线AD₁与抛物线C₂只有一个公共点A，
下面只要考虑直线AD₁与抛物线C₁的公共点个数．
联立直线AD₁和抛物线C₁的方程$\left\{\begin{array}{l}y=2x+2\\ y={mx}^{2}-2mx-3m\end{array}\right.$，故mx²-（2m+2）x-3m-2=0，
解得x₁=3+$\frac{2}{m}$，x₁=-1．
∵m＜0，
∴3+$\frac{2}{m}$＜3．
①当3+$\frac{2}{m}$＞-1，即m＜-$\frac{1}{2}$时，
直线AD₁与该蛋线有两个公共点；
②当3+$\frac{2}{m}$≤-1，即-$\frac{1}{2}$≤m＜0时，
直线AD₁与该蛋线只有一个公共点A．
综上所述，当m＜-$\frac{1}{2}$时，直线AD₁与该蛋线有两个公共点；
当-$\frac{1}{2}$≤m＜0时，直线AD₁与该蛋线有一个公共点．

点评 本题考查的是二次函数综合题，涉及到抛物线与x轴的交点、梯形的判定与性质、相似三角形的判定与性质邓州市，难度较大．