题目内容
6.小颖和小丽做“摸球”游戏:在一个不透明的袋子中装有编号为1-4的四个球(除编号外都相同),从中随机摸出一个球,记下数字后放回,再从中摸出一个球,记下数字.若两次数字之和大于5,则小颖胜,否则小丽胜,这个游戏对双方公平吗?请说明理由.分析 列表得出所有等可能的情况数,找出数字之和大于5的情况数,分别求出两人获胜的概率,比较即可得到游戏公平与否.
解答 解:这个游戏对双方不公平.
理由:列表如下:
| 1 | 2 | 3 | 4 | |
| 1 | (1,1) | (2,1) | (3,1) | (4,1) |
| 2 | (1,2) | (2,2) | (3,2) | (4,2) |
| 3 | (1,3) | (2,3) | (3,3) | (4,3) |
| 4 | (1,4) | (2,4) | (3,4) | (4,4) |
故小颖获胜的概率为:$\frac{6}{16}$=$\frac{3}{8}$,则小丽获胜的概率为:$\frac{5}{8}$,
∵$\frac{3}{8}$<$\frac{5}{8}$,
∴这个游戏对双方不公平.
点评 此题考查了游戏公平性,以及列表法与树状图法,判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
1.某种计算机完成一次基本运算的时间约为0.000 000 001s.把0.000 000 001s用科学记数法可表示为( )
| A. | 0.1×10-8s | B. | 0.1×10-9s | C. | 1×10-8s | D. | 1×10-9s |
3.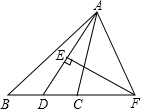 如图,在△ABC中,∠ABC=45°,AD是∠BAC的平分线,EF垂直平分AD交BC的延长线于F,则∠CAF的度数是( )
如图,在△ABC中,∠ABC=45°,AD是∠BAC的平分线,EF垂直平分AD交BC的延长线于F,则∠CAF的度数是( )
 如图,在△ABC中,∠ABC=45°,AD是∠BAC的平分线,EF垂直平分AD交BC的延长线于F,则∠CAF的度数是( )
如图,在△ABC中,∠ABC=45°,AD是∠BAC的平分线,EF垂直平分AD交BC的延长线于F,则∠CAF的度数是( )| A. | 30° | B. | 45° | C. | 75° | D. | 60° |
7. 如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=8,则四边形CODE的周长( )
如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=8,则四边形CODE的周长( )
 如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=8,则四边形CODE的周长( )
如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=8,则四边形CODE的周长( )| A. | 8 | B. | 12 | C. | 16 | D. | 20 |
8.下列运算,正确的是( )
| A. | 0.1-2=0.01 | B. | ($\frac{1}{2}$)-3=-8 | C. | (-2)-2=4 | D. | (mn-2)-1=$\frac{{n}^{2}}{m}$ |
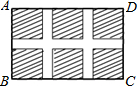 如图,小区计划在一个长为40cm,宽为26m的矩形场地ABCD上修建三条同样宽的路,使其中两条与AB平行,另一条与AD平行,其余部分种草,若使每一块草坪的面积都为144m2,求路的宽度.
如图,小区计划在一个长为40cm,宽为26m的矩形场地ABCD上修建三条同样宽的路,使其中两条与AB平行,另一条与AD平行,其余部分种草,若使每一块草坪的面积都为144m2,求路的宽度. 如图,AC=AE,∠1=∠2,AB=AD.求证:BC=DE.
如图,AC=AE,∠1=∠2,AB=AD.求证:BC=DE.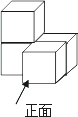 由4个相同的小立方体搭成的几何体如图所示,则它的主视图是( )
由4个相同的小立方体搭成的几何体如图所示,则它的主视图是( )