题目内容
7.如图,等腰直角△EFG的直角边GE与正方形ABCD的边BC在同一直线上,且点E与点B重合,△EFG沿BC方向匀速运动,当点G与点C重合时停止运动.设运动时间为t,运动过程中△EFG与正方形ABCD的重叠部分面积为S,则S关于t的函数图象大致为( )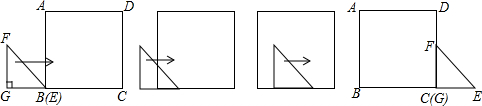
| A. |  | B. |  | C. |  | D. |  |
分析 设GF=BG=a,AB=BC=m,Rt△EFG向右匀速运动的速度为1,当E点与点B重合时,S=0;当点G在点B左侧,点E在点B右侧时,如图1,得到S是t的二次函数,且二次项系数为正数,所以抛物线开口向上;当点G在点B右侧,点E在点C左侧时,S=$\frac{1}{2}$a2;当点G在点B左侧,点E在点B右侧时,如图3,得到S是t的二次函数,且二次项系数为负数,所以抛物线开口向下,于是得到结论.
解答 解:设GF=BG=a,AB=BC=m,Rt△EFG向右匀速运动的速度为1,
当E点与点B重合时,S=0;
当点G在点B左侧,点E在点B右侧时,如图1,
BE=t,
∴S=$\frac{1}{2}$t2,
∴S是t的二次函数,且二次项系数为正数,所以抛物线开口向上;
当点G在点B右侧,点E在点C左侧时,如图2,S=$\frac{1}{2}$a2;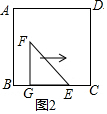
当点G在点B左侧,点E在点B右侧时,如图3,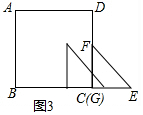
S=$\frac{1}{2}$a2-$\frac{1}{2}$(t-m)2,
∴S是t的二次函数,且二次项系数为负数,所以抛物线开口向下,
综上所述,S与t的图象分为三段,第一段为开口向上的抛物线的一部分,第二段为与x轴平行的线段,第三段为开口向下的抛物线的一部分.
故选A.
点评 本题考查了动点问题的函数图象:先根据几何性质得到与动点有关的两变量之间的函数关系,然后利用函数解析式和函数性质画出其函数图象,注意自变量的取值范围.

练习册系列答案
相关题目
19.表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数与方差s2.
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )
| 甲 | 乙 | 丙 | 丁 | |
| 平均数 x(cm) | 561 | 560 | 561 | 560 |
| 方差s2(cm2) | 35 | 35 | 155 | 165 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
 在△ABC中,已知∠C=90°,AC=6,BC=8.
在△ABC中,已知∠C=90°,AC=6,BC=8.