题目内容
6.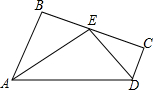 如图,AB∥CD,E点在BC上,AE平分∠BAD,DE平分∠ADC.求证:
如图,AB∥CD,E点在BC上,AE平分∠BAD,DE平分∠ADC.求证:(1)EB=EC;
(2)AB+CD=AD.(用两种方法)
分析 (1)延长AE,DC交于M,由平行线的性质得出∠DAB+∠ADC=180°,∠BAE=∠CME,由ASA证明△ADE≌△MDE,得出AE=ME,再由ASA证明△ABE≌△MCE,得出对应边相等即可;
(2)方法一:由全等三角形的性质得出AB=CM,证出∠CME=∠DAE,得出AD=DM,即可得出结论;
方法二:延长DE与AB的延长线交于一点F,由AAS证明△DCE≌△FBE,得出BF=DC,DE=EF,证出AD=AF,即可得出结论.
解答 证明:(1)延长AE,DC交于M,如图1所示: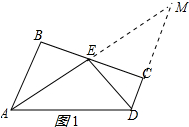
∵AB∥DC,
∴∠DAB+∠ADC=180°,∠BAE=∠CME,
∵AE、DE分别平分∠BAD、∠ADC,
∴∠EAD+∠ADE=90°,
∴∠AED=90゜=∠DEM,
在△ADE和△MDE中,
$\left\{\begin{array}{l}{∠ADE=∠MDE}\\{DE=DE}\\{∠AED=∠DEM}\end{array}\right.$,
∴△ADE≌△MDE(ASA),
∴AE=ME,
在△ABE和△MCE中,
$\left\{\begin{array}{l}{∠AEB=∠MEC}\\{AE=ME}\\{∠BAE=∠CME}\end{array}\right.$,
∴△ABE≌△MCE(ASA),
∴EB=EC;
(2)方法一:由(1)知:△ABE≌△MCE,
∴AB=CM,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠CME=∠DAE,
∴AD=DM,
∵DM=CM+CD=AB+CD,
∴AB+CD=AD;
方法二:延长DE与AB的延长线交于一点F,如图2所示: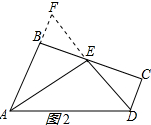
∵AB∥CD,
∴∠CDE=∠BFE由(1)知:BE=CE,
在△DCE和△FBE中,
$\left\{\begin{array}{l}{∠CDE=∠BFE}\\{∠DEC=∠FEB}\\{BE=CE}\end{array}\right.$,
∴△DCE≌△FBE(AAS),
∴BF=DC,DE=EF,
∴AF=AB+BF=AB+CD,
∵AE平分∠BAD,
∴∠ADF=∠AFD,
∴AD=AF,
∴AB+CD=AD.
点评 本题考查了全等三角形的判定与性质、等腰三角形的判定与性质、平行线的性质等知识;本题综合性强,有一定难度,需要通过作辅助线证明三角形全等才能得出结论.

 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案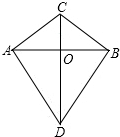 如图,CA=CB,DA=DB.求证:OA=OB,CD⊥AB.
如图,CA=CB,DA=DB.求证:OA=OB,CD⊥AB.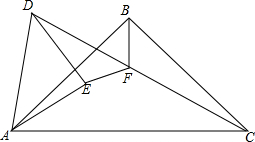 如图,等腰直角△ABC中,∠ABC=90°,等腰直角△ADE中,∠AED=90°,AE<AB,点E在△ABC内部,点F是CD的中点,猜想EF和BF的数量和位置关系,并说明理由.
如图,等腰直角△ABC中,∠ABC=90°,等腰直角△ADE中,∠AED=90°,AE<AB,点E在△ABC内部,点F是CD的中点,猜想EF和BF的数量和位置关系,并说明理由. 如图,在等边三角形中,D为BC上一点,BD=2CD,DE⊥AB于E,CE交AD于P.
如图,在等边三角形中,D为BC上一点,BD=2CD,DE⊥AB于E,CE交AD于P.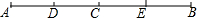 如图,已知点C是线段AB的中点,点D是线段AC的中点,点E是线段BC的中点.
如图,已知点C是线段AB的中点,点D是线段AC的中点,点E是线段BC的中点.