题目内容
3.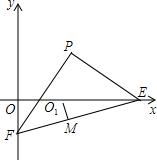 如图,P(1,1),PE⊥PF,O为△OEF的内角平分线的交点,O1M⊥EF于M.
如图,P(1,1),PE⊥PF,O为△OEF的内角平分线的交点,O1M⊥EF于M.(1)求证:2O1M=OE+OF-EF;
(2)若ME、MF的长度分别为x2-mx+2m-1=0的两根,求m的值.
分析 (1)过O1作O1A⊥x轴于A,O1B⊥y轴于B,连接O1E,O1F,得到O1A=O1B=O1M,推出四边形OAO1B是正方形,根据正方形的性质得到O1A=O1B=OA=OB=O1M,证得Rt△AO1E≌△RtMO1E,同理Rt△BO1F≌△RtMO1F,根据全等三角形的性质得到AE=ME,BF=MF即可得到结论;
(2)过P作PC⊥x轴于C,PD⊥y轴于D,得到PC=PD=1=OC=OD,证得△PDF≌△PCE,根据全等三角形的性质得到DF=CE,求得OF=DF-OD=CE-1=OE-OC-1=OE-2,得到ME=MF=AE-BF=(OE-OA)-(OF-OB)=OE-OF=2,求得(ME-MF)2=4,即(ME+MF)2-4ME•MF=4,根据ME、MF的长度分别为x2-mx+2m-1=0的两根,于是得到ME+MF=m,ME•MF=2m-1,即可得到结论.
解答 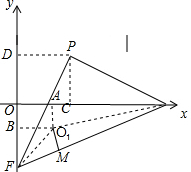 解:(1)过O1作O1A⊥x轴于A,O1B⊥y轴于B,连接O1E,O1F,∴O1A=O1B=O1M,∵∠O1AO=90°,∠O1BO=90°,∠AOB=90°,
解:(1)过O1作O1A⊥x轴于A,O1B⊥y轴于B,连接O1E,O1F,∴O1A=O1B=O1M,∵∠O1AO=90°,∠O1BO=90°,∠AOB=90°,
∴四边形OAO1B是正方形,
∴O1A=O1B=OA=OB=O1M,
在Rt△AO1E与△RtMO1E中,
$\left\{\begin{array}{l}{A{O}_{1}=M{O}_{1}}\\{{O}_{1}E={O}_{1}E}\end{array}\right.$,
∴Rt△AO1E≌△RtMO1E,同理Rt△BO1F≌△RtMO1F,
∴AE=ME,BF=MF,
∴2O1M=OA+OB=OE-AE+OF-BF=OE+OF-ME-MF=OE+OF-EF;
(2)过P作PC⊥x轴于C,PD⊥y轴于D,
∴PC=PD=1=OC=OD,
∵∠CPD=90°,∠EPF=90°,
∴∠DPF=∠CPE,
在△PDF与△PCE中,
$\left\{\begin{array}{l}{∠PDF=∠PCE}\\{PD=PC}\\{∠DPF=∠CPE}\end{array}\right.$,
∴△PDF≌△PCE,
∴DF=CE,
∴OF=DF-OD=CE-1=OE-OC-1=OE-2,
∴ME-MF=AE-BF=(OE-OA)-(OF-OB)=OE-OF=2,
∴(ME-MF)2=4,即(ME+MF)2-4ME•MF=4,
∵ME、MF的长度分别为x2-mx+2m-1=0的两根,
∴ME+MF=m,ME•MF=2m-1,
∴m2-4(2m-1)=4,
解得:m=8,或m=0(舍去),
∴m的值是8.
点评 本题考查了全等三角形的判定和性质,坐标与图形的性质,正方形的性质,一元二次方程根与系数的关系,正确的作出辅助线是解题的关键.

 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案| 种群 | 蚂蚁、蜜蜂和黄蜂 | 甲虫、象鼻虫 | 蝴蝶、蛾 | 苍蝇、蚊子 | 其他昆虫 |
| 种数/万 | 10 | 30 | 11 | 10 | 15 |
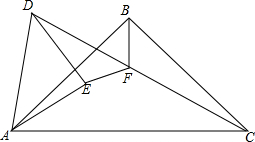 如图,等腰直角△ABC中,∠ABC=90°,等腰直角△ADE中,∠AED=90°,AE<AB,点E在△ABC内部,点F是CD的中点,猜想EF和BF的数量和位置关系,并说明理由.
如图,等腰直角△ABC中,∠ABC=90°,等腰直角△ADE中,∠AED=90°,AE<AB,点E在△ABC内部,点F是CD的中点,猜想EF和BF的数量和位置关系,并说明理由. 如图,在等边三角形中,D为BC上一点,BD=2CD,DE⊥AB于E,CE交AD于P.
如图,在等边三角形中,D为BC上一点,BD=2CD,DE⊥AB于E,CE交AD于P.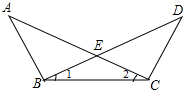 已知:如图,∠A=∠D,∠1=∠2,你能证明图中哪些线段相等?哪些角相等?
已知:如图,∠A=∠D,∠1=∠2,你能证明图中哪些线段相等?哪些角相等?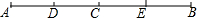 如图,已知点C是线段AB的中点,点D是线段AC的中点,点E是线段BC的中点.
如图,已知点C是线段AB的中点,点D是线段AC的中点,点E是线段BC的中点.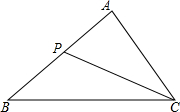 如图,已知△ACP∽△ABC,AC=6,AP=3,则AB的长为12.
如图,已知△ACP∽△ABC,AC=6,AP=3,则AB的长为12.