题目内容
10．已知函数y=$\frac{k}{x}$的图象过点（1，-2），则该函数的图象必在（ ）| A． | 第二、三象限 | B． | 第二、四象限 | C． | 第一、三象限 | D． | 第三、四象限 |
分析 先将点（1，-2）代入函数解析式y=$\frac{k}{x}$，求出k的取值，从而确定函数的图象所在象限．
解答 解：∵函数y=$\frac{k}{x}$的图象过点（1，-2），
∴-2=$\frac{k}{1}$，k=-2，
∴函数解析式为y=-$\frac{2}{x}$，
∴函数的图象在第二、四象限．
故选：B．
点评 本题考查了反比例函数的图象与性质：k＞0时，图象在第一、三象限；k＜0时，图象在第二、四象限；以及待定系数法求函数解析式．
练习册系列答案
相关题目
1．下列命题正确的有（ ）
①若ac=bc，则a=b；②同位角相等；③x+1=1是一元一次方程；④若x2=9，则x=3；⑤过一点有且只有一条直线与已知直线垂直；⑥直线外一点到这条直线的垂线段叫做点到直线的距离．
①若ac=bc，则a=b；②同位角相等；③x+1=1是一元一次方程；④若x2=9，则x=3；⑤过一点有且只有一条直线与已知直线垂直；⑥直线外一点到这条直线的垂线段叫做点到直线的距离．
| A． | 0个 | B． | 1个 | C． | 2个 | D． | 3个 |
5．
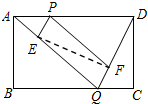如图所示，已知矩形ABCD的边长AB=2，BC=3，点P是AD边上的一动点（P不同于A、D），Q是BC边上的任意一点，连接AQ、DQ，过P作PE∥DQ交AQ于E，作PF∥AQ交DQ于F．设AP的长为x，则△PEF的面积y关于x的函数关系式是（ ）
如图所示，已知矩形ABCD的边长AB=2，BC=3，点P是AD边上的一动点（P不同于A、D），Q是BC边上的任意一点，连接AQ、DQ，过P作PE∥DQ交AQ于E，作PF∥AQ交DQ于F．设AP的长为x，则△PEF的面积y关于x的函数关系式是（ ）| A． | y=-$\frac{1}{3}$x2+x | B． | y=-$\frac{2}{3}$x2+2x | C． | y=-$\frac{1}{3}$x2+x+3 | D． | y=-$\frac{2}{3}$x2+2x+6 |
15．迄今为止，科学家发现了约76万种昆虫，这张表表示昆虫的主要类群种数．利用这些数据，绘制一张扇形图，来表示每种昆虫所占的百分比．
| 种群 | 蚂蚁、蜜蜂和黄蜂 | 甲虫、象鼻虫 | 蝴蝶、蛾 | 苍蝇、蚊子 | 其他昆虫 |
| 种数/万 | 10 | 30 | 11 | 10 | 15 |
如图，在等边三角形中，D为BC上一点，BD=2CD，DE⊥AB于E，CE交AD于P．